強化学習：行動価値関数（Action Value Function）（実装・写経）

Bellman方程式 行動価値 強化学習

f:id:shirakonotempura:20190131003939p:plain

今回は、前２回で整理した状態価値関数V^\pi(s)と同じ価値関数である行動価値関数（Action Value Function）について整理していきます．

以下を参考にしています．以下の記事はかなり丁寧に書かれていますが、だいぶはしょっていきます． qiita.com

行動価値関数と状態価値関数

状態価値関数V^\pi(s)は、状態sが持つ価値を表していました．

各状態の価値が分かれば、その状態を選ぶ行動がベストな行動なわけなのですが、V^\pi(s)は、変数に行動aを持っておらず、直接取るべき行動が示されているわけではありません．

一方、今回勉強する行動価値関数は、状態sでの行動aを評価する関数であり、ある状態sが与えられたとき、どの行動が最適な行動なのか、ということを知ることができます．

定義：

以下に、２つの価値関数の定義を示します．

状態価値関数V^\pi(s)：状態sにあるときに、方策\piに従ったときの価値

行動価値関数Q^\pi(s, a)：状態sにおいて、行動aを取った後、方策\piに従ったときの価値

行動価値関数の行動aは方策\piに従ったものではありません．つまり、状態sにおける最初の行動は方策に従わずに決めます．

行動価値関数の定式化

Q^\pi(s, a)を定式化していきます． 導出にあたり設ける仮定を以下に示します．

  • 方策\piが決まっている
  • 現在の時刻tでは、方策\piに従わず、行動aを取り時刻t+1で状態s'に遷移する
  • 時刻t+1後の行動は、方策\piに従って行動する

ダイアグラムを以下に示します． f:id:shirakonotempura:20190130094415p:plain

時刻tにおける状態価値関数V^\pi(s)については、今は無視します．状態s、時刻tでとった行動aに対する行動価値関数Q^\pi(s, a)を起点に考えます．

行動aを選択した後、遷移確率P^a_{ss'}によって確率的に遷移します（図中青で示した分岐）．その遷移後の状態価値がV^\pi(s')です．

図中では、その後さらにポリシー\piで分岐、遷移確率Pでの分岐と枝分かれが続いていますが、行動価値関数Q^\pi(s, a)の数式にその先を考える必要はありません．状態価値がV^\pi(s')に枝分かれ以降で得られる報酬の総和（収益）になっているからです．以下に状態価値V^\pi(s')を使った行動価値関数Q^\pi(s, a)の計算式を示します．

$$Q^\pi(s,a) = \sum{s'} P^a_{ss'}[R^a_{ss'} + \gamma V^\pi(s')] \qquad \cdots \qquad (2)$$

R^a_{ss'}は、状態sで行動aをとり、次の状態s'に遷移したときの報酬を示します．

状態価値関数から見た行動価値関数

先ほど、『今は無視します』とした現時刻における状態価値V^\pi(s)を起点にみた場合の、行動価値関数との関係を考えてみます．以下にダイアグラムを示します．

f:id:shirakonotempura:20190131000309p:plain

状態価値関数V^\pi(s)から、方策\pi(s,aに従って行動が選択されていますので、以下のような式で表すことができます．

$$V^\pi(s) = \sum_{a} \pi(s,a) Q^\pi(s,a) \qquad \cdots \qquad (3)$$

1ステップ先の行動価値関数

次に、行動価値関数同士（現在と次のSTEP）の関係を考えてみます．これは、上で説明した式(2)を式(3)に代入すれば表すことができます．

$$Q^\pi(s,a) = \sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma\sum_{a}\pi(s',a')Q^{\pi}(s',a')] \qquad \cdots \qquad (4)$$

上式の関係は以下のダイアグラムのようになります． f:id:shirakonotempura:20190131002232p:plain

式のまとめ

行動価値関数と前回導出した状態価値関数の数式を以下にまとめます．

状態価値関数（前回求めたもの）

$$V^\pi(s) = \sum_a\pi(s,a)\sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma V^{\pi}(s')]　\quad \cdots \qquad (1)$$

行動価値関数

$$Q^\pi(s,a) = \sum{s'} P^a_{ss'}[R^a_{ss'} + \gamma V^\pi(s')] \qquad \cdots \qquad (2)$$

状態価値関数と行動価値関数の関係

$$V^\pi(s) = \sum_{a} \pi(s,a) Q^\pi(s,a) \qquad \cdots \qquad (3)$$

1ステップ先の行動価値関数（更新式）

$$Q^\pi(s,a) = \sum_{s'}P_{ss'}^a[R_{ss'}^a + \gamma\sum_{a}\pi(s',a')Q^{\pi}(s',a')] \qquad \cdots \qquad (4)$$

実装

では、こちらのコードを写経させてもらい実際にAction Valueの計算を行ってみました．
問題設定は、これまでと同じGrid Worldを使用し、枝分かれは10ステップ先まで考慮しています．なお、ポリシー\piはあくまでランダム（上下左右等確率）です．

結果

以下に行動価値関数Q^\pi(s,a)の計算結果を示します．コードを使わせてもらったら、図の出力まで完璧でした．こんな図が描けるようになりたい・・・．
各状態sに対して上下左右4つの行動がありますので、Q^\pi(s,a)も1つのグリッドに対して4つ計算されています．グリッドAおよびBにおいては、どの行動をとっても得られる報酬と次の状態が同じであるため、Q(s,a)に差はありません．

f:id:shirakonotempura:20190131005834p:plain

各状態において、最も大きな値の行動が、その状態でとる計算上のベストな行動になります．Q値が大きい行動を赤矢印にしたものが以下になります．

f:id:shirakonotempura:20190131005934p:plain

まとめ

  • 行動価値Q^\pi(s,a)の定式化を行いました
  • Grid Worldの問題に行動価値の計算を実装し、ランダムに動くポリシー\piの元での行動価値関数Q^\pi(s,a)を求めました．

繰り返しになりますが、今回の計算もあくまでポリシー自体は固定（ランダム移動）で行っています．強化学習の目的は『長期的に得られる収益を最大化する方策』を見つけることですが、まだポリシーを改善したわけではないのです．

今回、ある方策のもとでのベストな行動は得る方法は分かりましたので、各状態のベスト行動を方策にしてまた行動価値を求めてという計算を繰り返し続ければ、いずれ最適な方策が得られそうな気はします．まあそれでは計算回数が多くなりそうですね．

強化学習：状態価値関数とBellman方程式 （実装・写経）

Bellman方程式 強化学習 状態価値 マルコフ決定過程

前回、コチラの記事を参考のまま、状態価値関数の定式化を行いましたので、実際にプログラムに実装して状態価値関数の計算を行ってみます．

今回も前回と同様の記事を参考にしています． qiita.com

この記事は私の学習用ノートです。上の記事をトレースしていることはご了承ください

今回の記事でまとめること

  • 状態価値関数V^\pi(s)の実装

前回の要約

前回は、状態価値関数V^\pi(s)を以下のように定式化しました．式の中身は『状態価値関数は、直近の報酬に1ステップ先の状態価値関数を足したものである．ただし、方策および遷移確率で未来の取りうる値は枝分かれするので、その期待値をとる』という内容になっています．

$$V^\pi (s) = \sum_{a} \pi(s,a) \sum_{s'}P^a_{ss'} [R^a_{ss'} + \gamma V^\pi (s')]$$

ここで、

  • \pi(s, a)：は方策と呼ばれ、状態sのときに各行動aをとる確率
  • P^a_{ss'}：は状態sで行動aを取った時に、状態s'に遷移する確率
  • R^a_{ss'}：は状態sで行動aを取り、状態s'に遷移したときに得られる報酬

となります．それぞれの関係をダイアグラムで描くと以下のように表せます．

f:id:shirakonotempura:20190126165021p:plain

Grid World

実装で対象とする問題では、前回Grid Worldとして紹介した5×5グリッドの格子状の世界を考えます．
以下、仮定のおさらいです．

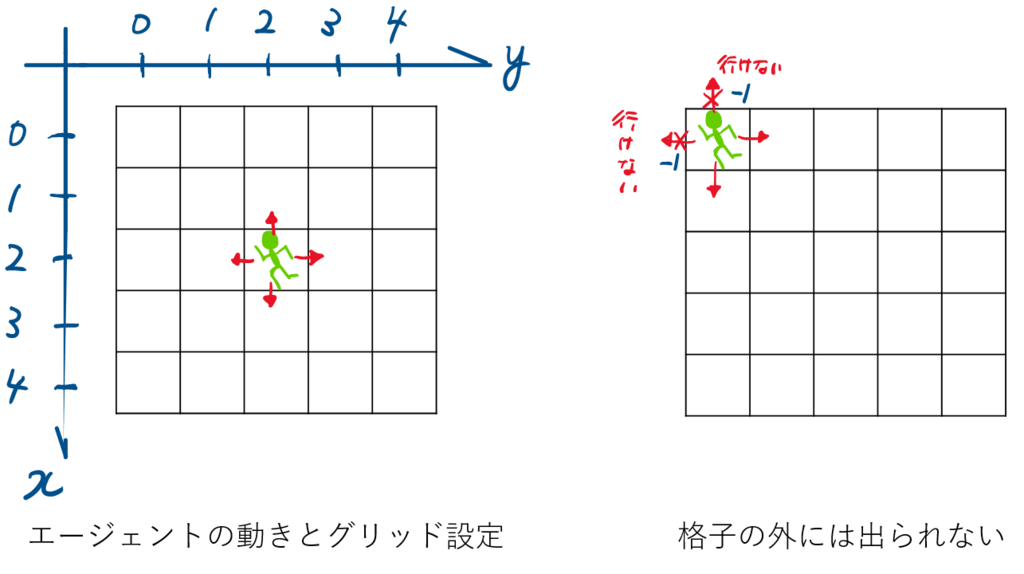
  • エージェントは、状態（＝どのグリッドにいるか）に関わらず、上下左右にランダムに1マス移動する方策に従って行動を起こします．
  • 遷移確率（[tex:P^a_{ss'}）は確定的とし、選んだアクションに応じて、必ずそのアクションを起こすものとします．
  • グリッドの外に出ることはできず、外にでる方向に移動しようとした場合、‐1の負の報酬が与えられ、エージェントの位置は変わらない
  • 図中AおよびBに移動した場合、その行動によらず次のステップでA’およびB'にワープする．その際、それぞれ+10および+5の報酬が与えられる．

f:id:shirakonotempura:20190126155117p:plain

f:id:shirakonotempura:20190126160041p:plain

実装

実装自体は、完全に写経なので元の記事を参考にしてください．

前回も触れましたが、今回の問題設定では終了条件がなく永遠にステップが続きます．そこで、割引率\gammaを使って未来に行くほど報酬を割引いています．今回は、計算コストの関係上11ステップ先（つまりS_{t+11}）まで考慮して、状態価値の計算を行っています．

結論から言うと、これではかなり不十分で、Suttonの本に載っている状態価値関数とは結構違っています．

結果

以下に11ステップまで考慮して求めた状態価値を示します．

f:id:shirakonotempura:20190130075123p:plain

唯一報酬が得られるグリッドAおよびBの状態価値が大きく、その周辺のグリッドも高い値になっていることが分かります．一方で、外側に出ようとする可能性が高く、報酬が得られる確率も低い下側のグリッドは総じて報酬が低くなっています．

グリッドAからA'にワープする際に得られる報酬が+10であるにも関わらず、Aの状態価値が10より低い理由は、ワープ後のA'の位置では負の報酬を得る確率が高く、その影響を受けているためです．一方、グリッドBの場合は、B'の一は画面中央付近で、負の報酬を得る確率は高くないのでAと異なり、状態価値は報酬の値（+5）より大きくなっています．

比較のため、Suttonの本に載っている状態価値の値を以下に示します．

f:id:shirakonotempura:20190130070338p:plain
出典：Reinforcement Learning：An Introduction

こちらは無限ステップ先まで考慮した（ちゃんと収束した）状態価値になっています（こちらをどうやって求めたんでしょう・・）．先にも言ったように、まだかなり差異が見られます．つまり、十分収束したと言えるほど計算ができていません．11ステップ先、枝分かれとして4^{11}通り（約400万通り）まで考慮しているので十分かと思っていましたが、11ステップ先では割引率はあまり低減されていなくて $$\gamma^{11} \simeq 0.31$$ と、まだ30%の寄与度を持っています．つまり、もう考慮してもしなくてもほぼと言えるステップはまだ先だということになります．仮に寄与度1%以下にまで落とそうとすると $$ x > \log_{0.9} 0.01$$ より44ステップ先まで考慮する必要があります・・・．その枝分かれ数たるや、遷移確率を確定的なものとしたとしても $$4^{44} = 3.09×10^{26}!!!$$ なんと、1兆×1兆通りを軽く超えてしまいます．これが次元の呪いというやつなんでしょうか・・．なんと、おそろしい．

結論としては、状態価値をこのやり方で十分と言えるまで計算しきることは現実的には難しそうです．

まとめ

定式化した状態価値V^\pi(s)を実装して実際にGrid Worldの状態価値を計算してみました．
状態価値の傾向は表せましたが、精度を上げるには別の工夫・やり方が必要なようです．

強化学習：状態価値関数とBellman方程式 (良記事のトレース）

強化学習 マルコフ決定過程 Bellman方程式 状態価値 行動価値

いきなりですが、状態価値関数・Bellman方程式について調べたくてこの記事にたどり着いた方は、何も考えずに以下の記事に飛んでください．時間を無駄にしなくてすみます．

qiita.com

今回から、上のQiitaに投稿された記事をトレースしながら状態価値関数からできればTD学習まで理解していきたいと思います．（絵はできるだけ自分で作成するようにしますが、描き方は参考にさせてください）

この記事は私の学習用ノートです．トレースです．元の記事は↑です．

今回の記事でまとめること

  • 状態価値関数V^\pi(s)の導出
  • 格子世界（Grid World）の状態価値関数の計算（Sutton本の3.5章）

特に後者は、本当にどうやって計算しているのかイメージできなかったので本当にありがたかったです．前者の導出もかなり丁寧に説明されています．

格子世界（Grid World）

今回の設定であるGrid Worldについて説明します．強化学習の例題で良く出てくるこの格子状のマス目の世界はGrid Worldと呼ばれています．

今回は5×5グリッドの世界を考えます．エージェントの上下左右に1マスずつ動きます（斜め方向は動きません）．

下図のように、x軸およびy軸は０から始まります．原点と正の向きについては、実際にGrid Worldを実装していく段階で重要になってきますので間違えないようにする必要があります．
エージェントはグリッドの外へ出ることはできません．出ようとする行動を選択することはありますが、その場合ペナルティとして負の報酬（-1）が与えられます．

f:id:shirakonotempura:20190126155117p:plain

図のAおよびBに到達した場合、その次の行動によらずAからはA'へ、BからはB'の状態に遷移します．その際、状態Aでとる行動には＋10の報酬が得られます．状態Bでとる行動には+5の報酬が与えられます．
恥ずかしながら、まずここの説明がテキストだけではよく理解できなかった．この説明のおかげでようやく問題の理解ができました．

f:id:shirakonotempura:20190126160041p:plain

その他、上記で明言していない行動に関しては、報酬は与えれません。（報酬０）

状態の価値

強化学習では、一般的にエージェントはあるポリシー\piに基づいて行動します．強化学習の目的は、長期的な収益を最大化するポリシーを求めることになります．

Grid Worldにおけるエージェントの場合だと

  • できるだけ上を多く選ぶ
  • 右に動いた後は、下を選ばない などがポリシーになります．

ということは、ご飯を食べた後すぐは運動しない、というのも人間のポリシーの１つですね．

話がそれましたが、状態の価値に話を戻します．今回のGrid Worldにおいてどの状態（グリッド）の価値が高いでしょうか．報酬がもらえるマスAやBの価値は間違いなく高そうです．となると、AやBに近いマスの価値も高くなりそうです．一方で、壁際のマスは、負の報酬を得る可能性があるので低くなってしまいそう．特に下側の方は、AやBからも遠いので価値は低そうな気がします．

それらの価値を求めるのが今回の目的になります．Sutton本ではいきなり価値関数が計算されているんですが、ちょっとはしょりすぎだと思いました．

このとき、状態の価値はポリシーによって変わるということに注意してください．例えば、オレは絶対右には動かない！というポリシーをエージェントが持っていたとすると、マスAの左にいることの価値は低くなります．

ポリシー（方策、戦略）の定式化

まず、ここでポリシーについて定式化をしておきます．

ポリシーは、ある状態sの時に行動aを取る確率として定義することができます．

Grid World上のある状態（ｘ=2, y = 3）において、右に0.7、その他に0.1ずつの確率で移動するという方策は

$$ \pi(s, a) = \left\{ \begin{array}{} 0.7 \qquad(s = (2, 3), a = right) \\ 0.1 \qquad(s = (2, 3), a = up) \\ 0.1 \qquad(s = (2, 3), a = left) \\ 0.1 \qquad(s = (2, 3), a = down) \end{array} \right.$$

となります．それぞれの状態sについて行動aそれぞれの確率を返すわけですから、全ての方策を配列に格納しようとすると、状態25×行動4＝100個の値が必要となります．これを

s\in S, a\in A, \pi \in S × Aと表したりします．

実際にポリシーの学習を行う場合には、各状態におけるポリシーを状態によらず同じ確率分布をとると設定することもよく行われます．

今回はこのポリシーの学習は行いません．というか、しばらく行いません．

今回のエージェントのポリシー： 『上下左右の行動はランダムに等確率で選択する』です

元記事でも書かれていますが、決まった方策のもとでの状態価値関数を導出するのが目的となります．

価値の定式化

ポリシーが定式化できましたので、いよいよ状態価値を定式化していきます．そのため、価値関数（Value Function）という概念を導入します．

価値関数は以下の2種類があります．

  • 状態価値関数（State Value Function)　V^\pi(s)

    • 状態s（にいることの）価値．

  • 行動価値関数（State Value Function)　Q^\pi(s,a)

    • 状態sにいて行動aを取ることの価値．Q^\pi(s,a)は行動に対して求められので、仮に今回の問題で求めるとすると1マスに対して4つのQ値が求まることになります．

今回は、状態価値関数V^\pi(s)を求めます．

では、情報価値の定式化にあたり、前回使用した強化学習のシステムを再度確認します．

f:id:shirakonotempura:20190126033017p:plain

時刻t（図の左端）に状態S_tにいたとき、ポリシー\piに従って行動A_tを取った結果、時刻t+1で状態S_{t+1}に遷移し、報酬R_{t+1}を受け取ります（このときの報酬はR_{t+1}であることに注意してください）．これを時々刻々繰り返していきます．

ここで、時刻tにおける状態S_tの状態価値V^\pi (S_t)を

『状態S_tを起点に、ポリシー\piに従って行動をとり続けた時の報酬の合計（つまり、収益）』

と定義してみます．

『とり続けた』と定義したように、終わりがくるまで永遠に行動をとり続けます．今回のGrid Worldの問題では終了条件はセットしていませんので、状態価値V^\pi (S_t)を求めるために、永遠に報酬を足し続けることになってしまいます．

当然、それでは計算が収束しませんので、前回登場した時間が経過するにつれて報酬を割り引く割引係数\gammaを使います．0 \leq \gamma \leq 1なので遠い未来ほど値が小さくなります．\gammaの大きさにより、未来をどれだけ重視するかを調整することができます．

f:id:shirakonotempura:20190126162521p:plain

上の図と同じように、時刻t+1を起点として、V^\pi (S_{t+1})についても考えてみましょう．１つ右にずれるだけですので、難しくないはずです．

f:id:shirakonotempura:20190126162543p:plain

では、再度時刻tにおけるV^\pi (S_t)を考えます．時刻t+1以降の報酬はV^\pi (S_{t+1})に集約されていますので、V^\pi (S_{t+1})を使えば以下のようにV^\pi (S_t)が書けるような気がします．

$$V^\pi (S_t) = r_{t+1} + \gamma V^\pi (S_{t+1})$$

かなり、すっきりとした式になりました．ある時刻における価値関数は、その先の時刻における価値関数の漸化式になっているようです．

しかし、厳密にはこの式は成立しません．価値関数が持つ性質の見落としがあるためです．以下で詳しく見ていきます．

正しい価値関数の導出

方策による枝分かれ

先に示したダイアグラムでは２つの見落としがありました．1つ目は

ある状態sからポリシー\piに従ってとる行動aは一義的には決まらない

ということです．ポリシーの説明で、ある状態での行動は確率的に決められると書いたように、他の行動が選ばれる可能性もあったということになります．当然、実際に選択して行動にうつすのは1つだけなのですが、行動を決める際には他の行動が取られる可能性が存在し、それが選択されたと場合の未来も存在していたということになり、以下のように枝分かれした未来を考慮する必要があります．

f:id:shirakonotempura:20190126165038p:plain

遷移確率による枝分かれ

さらに見落としている分岐がもう１つあります．それは

状態sでポリシー\piに従って行動aが選ばれたとき、それに対応する状態s'は一義的には決まらない

ということです．エージェントがはれて右に行くという選択をしたのに、右に行くとは限らないなんて・・・．ですが、これも遷移確率（Transition Probability）というちゃんとした名前が付けられています．ポリシーの確率分布と混同しそうになりますが、例えば95%の確率で指示通りに動作するけど、たまに想定外の動作をするロボットなんかがイメージしやすいかもしれません。

任意の状態sと行動aが与えられた場合の、次に可能な各状態s'の確率は

$$P^a_{ss'} = P_r [s_{t+1} = s' | s_t = s, a_t = a]$$

と表されます．またその際の報酬はR^a_{ss'}と表します．方策による枝分かれにさらに遷移確率による枝分かれを考慮したダイアグラムは以下のようになります．

f:id:shirakonotempura:20190126165021p:plain

なんかめちゃくちゃ複雑になってしまいましたが、ようやく状態価値関数を正しく表す準備が整いました．

状態価値関数の導出とBellman方程式

あらためて、先ほど定義した状態価値関数の式を示します．

$$V^\pi (S_t) = r_{t+1} + \gamma V^\pi (S_{t+1})$$

こちらに見落としていた２つの枝分かれの影響を考慮していきます．

方策と遷移確率を考慮するためには、さきほどダイアグラムで示したようにとりうる分岐の全てを考慮して報酬を合計する必要があります．どのようにするかというと、それぞれの枝の重みに枝分かれがとる確率をあてはめていきます．つまり期待値を計算することになります．

上記を考慮して、状態価値関数の定式化を行うと以下のようになります．

$$V^\pi (s) = \sum_{a} \pi(s,a) \sum_{s'}P^a_{ss'} [R^a_{ss'} + \gamma V^\pi (s')]$$

この式を、日本語で訳してみると
状態価値関数は、直近の報酬に1ステップ先の状態価値関数を足したものである．ただし、方策および遷移確率で未来のとりうる値は枝分かれするので、その期待値をとる

このような漸化式を状態価値関数V^\piに対するBellman方程式と呼びます．

数式

最後に、Sutton本で書かれている状態価値関数の導出を載せておきます．元の記事でも書かれているように、この式を覚える必要はないかと思います．

$$\begin{eqnarray} V^\pi (s) &=& E_\pi [R_t|s_t = s] \\ &=& E_\pi \biggl[\sum_{k=0}^\infty \gamma^k r_{t+k+1}|s_t = s\biggr] \\ &=& E_\pi \biggl[r_{t+1} + \gamma \sum_{k=0}^\infty \gamma^k r_{t+k+2} | s_t = s\biggr] \\ &=& \sum_{a} \pi(s, a) \sum_{s'} P^a_{ss'} \biggl( R^a_{ss'} + \gamma E_\pi \biggl[ \sum_{k=0}^\infty \gamma^k r_{t+ k + 2} | s_{t+1} = s' \biggr] \biggr) \\ &=& \sum_{a} \pi(s,a) \sum_{s'}P^a_{ss'} [R^a_{ss'} + \gamma V^\pi (s')] \\ \end{eqnarray}$$

まとめ

Sutton本の3.5章～を理解するため、冒頭で紹介させていただいた記事のトレースしました．

次回は引き続きトレースをしながら、実際に状態価値を計算するコードの実装をしていきます．

数式の記法がだいぶ身に付きました・・（泣）

強化学習：Markov Decision Processes（マルコフ決定過程）

強化学習 MDPs マルコフ決定過程

はじめに

今回は、強化学習における最も重要な考え方の１つであるマルコフ決定過程について整理していきます．

目標

マルコフ決定過程（Markov Decision Processes）

強化学習の枠組み（再掲）

f:id:shirakonotempura:20190122035140p:plain

マルコフ決定過程の説明に先立ち、強化学習フレームワークにおける用語とその意味について再度示します．

エージェントと環境は、t = 0, 1, 2, \dotsにおいて、相互に影響を及ぼします

  • エージェントはステップtごとに状態S_tを獲得
  • ステップtにおける行動A_tを実行する
  • 行動A_tによって、報酬R_{t+1}を得る
  • 行動A_tによって、状態がS_tからS_{t+1}に変化する

強化学習のシステムは以下のように表されます． f:id:shirakonotempura:20190126033017p:plain

マルコフ決定過程

強化学習のタスクが、マルコフ性を満たす場合、そのタスクはマルコフ決定過程（Markov decision process，MDP）と呼ばれます．もし、行動と状態が有限であるなら、有限マルコフ決定過程と呼ばれます（Finite MDP）．

マルコフ決定過程のタスクにおいて、次の状態は、現在の状態Sと行動Aによって確率的に決定されます．その確率は、エージェントが状態sにおいて行動aを決定したとき、状態sが状態s'に遷移する確率として以下の用に表されます．

$$P(s' | s, a)$$

例えば、マルコフ決定過程のもとではt+1ステップ目における状態S_{t+1}はtステップ目の状態S_tと、その状態で選ばれた行動A_tにより、以下のように求めることができます．

$$S_{t+1} \sim P(s' | S_t, A_t)$$

このとき[tex:S{t+1}]は[tex:S{t-1}]やA_{t-1}などには依存せず、S_tとA_tのみに依存して定まることに注意が必要です．このように直前の状態によってのみ遷移確率が決まる性質のことをマルコフ性（The Markov Property）と言います．（この性質があるタスクは、マルコフ決定過程のタスクとして考えられるといった方が正しいと思います．）

また、現在の状態S_tと行動A_tおよび次の状態[tex:S{t+1}]に応じて、報酬[tex:R{t+1}]を次のように定めます．

$$R_{t+1} = r (S_t, A_t, S_{t+1})$$

報酬と収益（Rewards and Returns）

以前述べたように、強化学習の目的は長期的な報酬を最大化することである．すなわち、[tex: R{t+1}, R{t+2}, R_{t+3} \dots]を最大にする行動A_tを選択することです．

しかし、将来的に得られるであろう報酬と、今得られる報酬では後者に重みをおく方が現実的だと言えます．そこで、割引率（discount rate）を用いて、将来得られる報酬を割り引く方法がよく用いられます．割引率\gamma （ \gamma \in [0, 1)）を考慮した時刻tの収益G_tは以下のように表されます．

$$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} +\gamma^3 R_{t+4}+ \cdots $$

これにより、将来得られる報酬より現在得られる報酬を重視すると同時に、計算が発散しにくくなるというメリットもあります．

収益を計算してみましょう．

割引率と報酬から得られる収益を計算してみましょう．（間違っていたらご指摘ください．）

\gamma Reward Sequence Return
0.5 (or any) 1 0 0 0 \dots 1.0
0.5 0 0 2 0 0 0 \dots 0.5
0.9 0 0 2 0 0 0 \dots 1.62
0.5 -1 2 6 3 2 0 0 0 \dots 2.0

まとめ

マルコフ決定過程の概要および割引率の考え方について整理しました．

全然、価値関数の話に入れませんでした．次回から価値関数について整理していきます．

強化学習：Multi-armed Bandits（UCB）

バンディット問題 強化学習 UCB Gradient-Bandit

今回の記事も、本テキストの主に2.6章、2.7章を整理したものになります．今回は、UCBアルゴリズムについて扱います．

ε-greedy法と同じく行動選択のアルゴリズムになります．

UCBアルゴリズム

早速ですがUCBアルゴリズムの説明をしていきます．UCBとはUpper Confidence Boundの略になります．前回紹介した楽観主義に基づいたアルゴリズムの１つです．

式から分かる特徴としては、

  • 何度も選ばれている行動ほど選ばれにくくなる
  • すべての行動の選択回数が多くなってくるにつれて探索回数を減らすことができる

価値は小さいが選択回数が少ないアームがある場合は（それを選択する）探索を行うアルゴリズムになります．

$$A_t \dot{=} \underset {a}{\operatorname {argmax}}\Biggl[Q_t(a) + c\sqrt{\frac{\log t}{N_t(a)} } \Biggr]$$

ここで、

A_t：step tにおいて選択する行動
Q_t(a)：step t における行動aの価値
c：UCB用ハイパーパラメータ（２でOK？）
t：総step数（100step目であれば100）
N_t(a)：step t までに行動aが選択された回数

注意：『これからの強化学習』に載っているのは『UCB1アルゴリズム』です．よく似ていますが若干中身が異なります．

さくっと実装

UCB用コンストラクタの実装

これまでと同様、スロットが持つ10本のアームの中から最良アーム（長期的に報酬を最大化できるアーム）を選択することを学習させます．

今回あらたに必要となるのは、UCB用ハイパーパラメータcとなります．
またこれが定義されているか否かがUCBアルゴリズムを使うかどうかのフラグにもなります．

#Banditクラスの定義
class Bandit:
# @k_arm: # of arms
# @epsilon: probability for exploration in epsilon-greedy algorithm
# @initial: initial estimation for each action
# コンストラクタ
    def __init__(self, k_arm=10, epsilon=0., initial=0.,  true_reward=0.,
                 sample_averages =False,  step_size = 0.1, UCB_param = None):      
        self.k = k_arm # 腕の数
        self.indices = np.arange(self.k) # k個のインデックスを作成
        self.time = 0 # time 初期値0
        self.average_reward = 0 # （平均）報酬の初期値0
        self.true_reward = true_reward # 真の報酬(クラス定義で指定しなければ0)
        self.epsilon = epsilon # クラス定義で指定しなければ0
        self.initial = initial # クラス定義で指定しなければ0

        self.sample_averages = sample_averages
        self.step_size = step_size
        
        self.UCB_param = UCB_param

行動選択メソッドへUCBアルゴリズムを追加

ε-greedy法とも組み合わせて使えます．εを設定した場合は、確率εでUCBで行動選択、それ以外はランダムで行動選択を行います．

    # get an action for this bandit
    # 行動（アーム）選択メソッド
    def act(self):
        #（乱数がεより小さければ完全にランダム）
        if np.random.rand() < self.epsilon:
            return np.random.choice(self.indices)
        
        # UCB
        if self.UCB_param is not None:
            UCB_estimation = self.q_estimation + \
                     self.UCB_param * np.sqrt(np.log(self.time + 1) / (self.action_count + 1e-5))
            q_best = np.max(UCB_estimation)
            return np.random.choice([action for action, q in enumerate(UCB_estimation) if q == q_best])

        # qの推定値の最大値をq_bestとする
        q_best = np.max(self.q_estimation)
        # q がq_bestと一致する行動の中からランダムで1つ選ぶ
        return np.random.choice([action for action, q in enumerate(self.q_estimation) if q == q_best])

インスタンスの設定と学習の実行（simulate())

今回は、UCBアルゴリズム（ε=0）と、探索率を0.1および0.01としたε-greedy法の３つのインスタンスを作っています．価値推定法は共通で標本平均法としています．

学習STEPは1000でもよかったのですが、ε=0.01としたε-greedy法の学習が1000回では不十分だったので3000STEPとしています．

今回もbanditsリストに各インスタンスを格納して、simulate()に渡しています

def UCB(runs=2000, time=3000):
    bandits = []
    bandits.append(Bandit(epsilon=0, UCB_param=2, sample_averages=True))
    bandits.append(Bandit(epsilon=0.1, sample_averages=True))
    bandits.append(Bandit(epsilon=0.01, sample_averages=True))
    _, average_rewards = simulate(runs, time, bandits)

結果

以下に平均報酬の学習履歴を示します．

  • UCBアルゴリズムは収束性、平均報酬の両面で最も性能がよい結果となりました．

  • ε= 0.1のケースは、200 STEP目あたりまでは性能がよいですが、その後性能が頭打ちとなっています．

  • ε = 0.01のケースは最終的には平均報酬はUCBアルゴリズムと同程度まで上がっていますが、収束の速さで遅れをとる結果となりました．平均報酬に関しては、もう少しSTEP数をやれば逆転したかもしれません．

f:id:shirakonotempura:20190125043451p:plain

まとめ

バンディット問題にUCBアルゴリズムを実装しました．

テキストではUCBの次に、Gradient-Bandit**というアルゴリズムも紹介されていますが、まったく理解できそうにないのでとばさせてください．

今回は、以下を参考にさせていただきました．

強化学習：Multi-armed Bandits（非定常・楽観的初期値）

強化学習 バンディット問題 非定常 定常

今回の記事は、本テキストの主に2.5章からを整理したものになります．今回は、Non-stationary Problem（非定常問題）およびOptimistic Initial Values（楽観的初期値）について扱います．

Tracking a Non-stationary Problem

前回は、行動の真の価値が変化しない仮定（定常）のもと、多腕バンディット問題を扱いました．アームの真の価値は常に変わりませんでした．しかし、実際に時間変化を伴う現実の問題では必ずしもこれは適切ではありません． では、時間の経過とともに、行動の真の価値が変化する状態（Non-stationary Problem、非定常問題）を考えていきます．

真の価値が変化する非定常問題においては、遠い過去の報酬よりも直近の報酬に重みを置く方が理にかなっていると言えます．

もし、あなたがあるお菓子のCM担当者でイメージキャラクターにタレントを選ばなければならない場合、 過去に一発当たったタレントを、現在流行りのタレントと同様には扱わないかと思います．

f:id:shirakonotempura:20190124055328p:plain

このように非定常問題においては、これまで価値の推定で使用した標本平均という考え方が適切でなくなるため、違った方法で価値を推定する必要があります．最もよく使われる方法は、ステップサイズパラメータと呼ばれる定数を用いる方法で、下式で表されます

Q_{n+1} \dot{=} \; Q_n + \alpha [R_n - Q_n]

ここで、\alphaがステップサイズパラメータを示し、\alpha \in (0, 1]の定数となります．
（\alpha \in (0, 1]は、{0} \lt \alpha \leq 1 を意味します）

Q_{n+1}は、過去の報酬と最初の推定量Q_1の加重平均となります．

\begin{align} Q_{n+1} \dot{=} \; Q_n + \alpha [R_n - Q_n]\ &= \alpha R_n + (1 - \alpha)[\alpha R_{n-1} + (1 - \alpha)Q_{n-1}]\\ &= \alpha R_n + (1 - \alpha) \alpha R_{n-1} + (1 - \alpha)^2 Q_{n-1}\\ &= \dots \\ &= (1 - \alpha)^n Q_1 + \sum_{i = 1}^{n} \alpha (1 - \alpha)^{n - i} R_i\\ \end{align}

Optimistic Initial Values

前述の式のとおり、これまでの方法は最初の行動価値の推定量Q_1(a)にある程度依存（偏り( bias)を持つとも言われる）しています．これまでは、あまり深く考えずにQ_1(a) = 0としてきましたが、実は初期値の見積もり方は、結果に大きく影響することがあります．

例として最初に3回ずつスロットを回した結果で初期推定値を決める場合を以下に示します．
上図のように、初期推定値を真の価値より高く見積もってしまった場合は、試行が進むにつれ選択が誤っていたことに気が付くことができます．一方で、真の価値よりも初期推定値を低く見積もってしまった場合、それが最良の行動であるにも関わらず、他方の行動価値がその推定値を下回らなければ、最良の行動は選択されなくなってしまいます．

f:id:shirakonotempura:20190125013336p:plain
楽観的勘違いの例

f:id:shirakonotempura:20190125013318p:plain
悲観的勘違いの例

出典：これからの強化学習（一部改良）

このように初期値を楽観視する楽観主義の考え方の名前には、『不確かな時は楽観的に（optimism in face of uncertainty）』という名前が付けられおり、探索と利用のトレードオフにおいて重要な考え方であると言えます．

最も単純な楽観主義のアルゴリズムである楽観的初期値法を以下に示します．このアルゴリズムでは、学習前に各アームから報酬の最大値をK回観測していたとして、アームの推定価値を高く（楽観的な側）に見積もるというものです.

楽観的初期値法

報酬の最大値をr_{sup}とする 学習中に観測した結果に加え、各アームからr_{sup}の報酬がK回観測されていたと考えて、各アームの報酬の期待値を計算する $$\acute{\mu_i} = \frac{これまで腕\;i\;から得られた報酬の和\;+\;Kr_{sup}}{これまで腕\;i\;をプレイした回数\;+\;K} $$ \acute{\mu_i}が最大のアームを選ぶ

出典：これからの強化学習

ただし今回の実装では、このアルゴリズムは実装しておらず単に初期値に楽観的な値を入れるだけとしています．

実装して確認

初期値の影響を確認するために、Q_1(a) = 5として、再度多腕バンディット問題を解いてみます．今回は価値の推定に標本平均法ではなく、ステップサイズパラメータ（\alpha = 0.1）を導入してみます．

ステップサイズパラメータと初期推定値の実装

今回は、追加修正した箇所のみ示します．こちらをみながら真似しているだけです．

コンストラクタへステップサイズパラメータの追加

コンストラクタに、step_sizeを追加しています．同時に、標本平均法を採用するかどうかを、sample_averages = True or Falseで判別するようにしています．

class Bandit:
# @k_arm: # of arms
# @epsilon: probability for exploration in epsilon-greedy algorithm
# @initial: initial estimation for each action
# コンストラクタ
    def __init__(self, k_arm=10, epsilon=0., initial=0.,  true_reward=0.,
                 sample_averages =False,  step_size = 0.1):      
        self.k = k_arm # 腕の数
        self.indices = np.arange(self.k) # k個のインデックスを作成
        self.time = 0 # time 初期値0
        self.average_reward = 0 # （平均）報酬の初期値0
        self.true_reward = true_reward # 真の報酬(クラス定義で指定しなければ0)
        self.epsilon = epsilon # クラス定義で指定しなければ0
        self.initial = initial # クラス定義で指定しなければ0
        self.sample_averages = sample_averages
        self.step_size = step_size

stepメソッドの修正

self.q_estimation[action]の計算に、step_sizeを導入した方法を追加しています．

sample_average = Trueであれば、標本平均法を、そうでなければstep_sizeを用いた手法となります．

    def step(self, action):
        # generate the reward under N(real reward, 1)
        # 報酬を平均（真の報酬）、分散１の正規分布からランダムに作成（スロットも確率的だということ）
        reward = np.random.randn() + self.q_true[action]
        
        self.time += 1
        
        # 平均報酬は、
        self.average_reward = (self.time - 1.0) / self.time * self.average_reward + reward / self.time
        
        # 行動カウンターを更新
        self.action_count[action] += 1
        
        
        if self.sample_averages:
            self.q_estimation[action] = (self.action_count[action] - 1.0) / self.action_count[action] * self.q_estimation[action] + reward / self.action_count[action]
        else:
            self.q_estimation[action] += self.step_size * (reward - self.q_estimation[action])

        return reward

関数e_greedyの修正

こちらは、今回使いませんが、コンストラクタにsample_average（デフォルト False）を追加していますので、インスタンスの定義において、sample_average = True`を追加しています．

def e_greedy(runs=2000, time=3000):
    # epsilonのサイズでパラスタ（0はgreedy行動選択）
    epsilons = [0, 0.1, 0.01, 0.5, 1.0]
    bandits = [Bandit(epsilon=eps, sample_averages = True) for eps in epsilons]    
    best_action_counts, rewards = simulate(runs, time, bandits)

関数optimistic_initial()の追加

テキストの内容に、初期Q値0.5でε=0.5および初期Q値0でε=0の2つのインスタンスを追加で定義しています．

def optimistic_initial(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(epsilon=0,   initial=5, step_size=0.1))
    bandits.append(Bandit(epsilon=0,   initial=0, step_size=0.1))
    bandits.append(Bandit(epsilon=0.1, initial=5, step_size=0.1))
    bandits.append(Bandit(epsilon=0.1, initial=0, step_size=0.1))
    best_action_counts, _ = simulate(runs, time, bandits)

    plt.plot(best_action_counts[0], label='epsilon = 0, q = 5')
    plt.plot(best_action_counts[1], label='epsilon = 0, q = 0')
    plt.plot(best_action_counts[2], label='epsilon = 0.1, q = 5')
    plt.plot(best_action_counts[3], label='epsilon = 0.1, q = 0')
    
    plt.xlabel('Steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('./images/optimistic_initial.png')
    plt.close()

結果

下図は最良のアームを選択した割合の履歴を示しています．緑（ε=0,初期Q値=0）のラインおよび紫（ε=0.1, 初期Q値=0）は前回示した図とほぼ同じものになります．

青（ε=0.0, 初期Q値=5）および赤（ε=0.1, 初期Q値=5）が初期値を５に設定した学習結果になります．150ステップあたりまでは、探査を多く行うため性能は高くありませんが、最終的には非常に良い性能を示しています．

青と紫を組み合わせた赤（ε-greedyかつ楽観初期値）が最も性能が良いのかと思っていましたが、そういうものではないのですね．難しい．

f:id:shirakonotempura:20190124225357p:plain

ちなみに、初期値を-5（悲観的？）としたケースも試しに行いました． 探索なしのケースでは、悲観的な推定価値から抜け出せずにいることが分かります．ε-greedyと組み合わせた場合は、何とか抜け出そうとしていますが、効率がだいぶ落ちていることが分かります．

f:id:shirakonotempura:20190125014110p:plain

まとめ

非定常問題への追従と楽観的初期値の考え方について整理しました．

以下を参考にさせていただきました．

強化学習その1

reinforcement-learning-an-introduction/chapter02 at master · ShangtongZhang/reinforcement-learning-an-introduction · GitHub

強化学習：Multi-armed Bandits（多腕バンディット問題）

強化学習 バンディット問題 Multi-arm Bandits Reinforcement Learning

はじめに

今回は先日紹介した強化学習の本の２章に登場するMulti-armed Banditsをとりあげます．
２章で取り上げられているので問題としては非常に単純な問題なのですが、いまだに研究の題材としては度々扱われます．2018年12月に開かれた国際会議NeurIPS 2018においてもBandit問題を扱った発表は多数見られました．

以下では、大学の講義ノートも参考にしながらバンディット問題を解説していきます．

Multi-armed Banditsとは

あたり（報酬）がでる確率の異なるアーム（スロットマシンをガチャンとやるアレです）を複数持つスロットがあると仮定します．プレイヤーはどのアームのあたり確率が高いかを知りません．

当然、プレイヤーはできるだけあたりの確率が高いアームだけを選び続けたいと考えます．同時にできるだけ早くそのアームを知りたいはずです． 一般化して書けば限られた試行回数の中で、最良の選択を探すことが、が多腕バンディット問題で達成したい目的になります．

補足：k本の腕とせず、1本の腕を持つk台のマシンとして説明される場合もありますが、同じことです．今回は本に従い、k本の腕を持つマシンを仮定して進めていきます．

  • 例１）k本の腕を持つマシンから1本を選んでN回プレイ、最良の腕を見つける
  • 例２）k台のマシンから1台を選んでN回プレイ、最良の台を見つける

行動価値の計算

q_*(k)を、アームkが持つ価値だとします．以下の４つのアームについて、価値を計算してみましょう．

  • １番のアーム：常に報酬８が得られる

    • 1番のアームの価値はq_*(1) = 8

  • ２番のアーム：88%の確率で報酬０、12%の確率で報酬１００が得られる

    • 2番のアームの価値はq_*(2) = .88 * 0 + .12 * 100 = 12

  • ３番のアーム：報酬は-10から35までの間で、等確率でランダムに等しく得られる．

    • 3番のアームの価値はq_*(3) = (-10 + 35) / 2 = 12.5

  • ４番のアーム：1/3の確率で報酬０、1/3の確率で報酬２０、1/3の確率で{8, 9, ..., 18}から等確率でランダム

    • 4番のアームの価値はq_*(4) = 1/3 * 0 + 1/3 * 20 + 1/3 * (8 + 18) /2 = 11

そのアームの価値、つまり選んだ行動kの価値は得られる報酬の期待値で計算することができます．
上の計算は合っていると思いますが、間違っていたらご指摘ください．

The k-armed Bandit Problem（k-armed バンディット問題）

繰り返しになりますが、数式をいれて再度バンディット問題を整理します． 時間ステップt = 1, 2, 3, \dotsにおいて、ｋ個の選択肢の中から１つを選び（A_t）、A_tに対して報酬R_tを得られるとします．

行動aの真の価値q_*(a)は、以下のように行動aで得られる報酬の期待値として計算されます

$$q_*(a) \dot{=} \boldsymbol{E}[R_t | A_t = a], 　 \forall_a \in [1, \dots, k] 　true values $$

プレイヤー（腕を選んでスロットを回す人）は、アームの真の価値および分布を知りません．にもかかわらず、プレイヤーは得られる報酬を最大化しなければなりません．つまり、できるだけベストなアームを選び続けつつ、各アームの価値を探る必要があります．この２つはトレードオフの関係にあり、探索と利用のジレンマ（Exploration and Exploitation Dilemma）と呼ばれます．

The Exploration/Exploitation Dilemma

時刻tにおけるgreedy（貪欲）行動a_tを次のように定義します．

$$ Q_t(a) \dot{=} \underset {a} {\operatorname {argmax}} Q_t(a)$$

ここで、
A_t = A_t^* なら、利用（exploiting)

A_t \neq A_t^* なら、探索（exploring)

プレイヤーは利用と探索の両方を同時にはできませんが、この両方をバランスよく必要があります．

行動価値Q_t(a)について

探索と利用のバランスよく行う方法の説明の前に、行動価値Q_t(a)について整理します．

バンディット問題における行動価値Q_t(a)は以下のように書くことができます．

$$Q_t(a) \dot{=} \frac{sum\; of\; rewards\; when\; a\; taken\; prior\; to\; t}{number\; of\; times\; a\; taken\; prior\; to\; t} = \frac{\sum_{i = 1}^{t - 1}R_i・\boldsymbol{1}_{A_i = a}}{\sum_{i=1}^{t-1} \boldsymbol{1}_{A_i = a}}$$

標本平均は無限回の試行が行われる場合、真の値に収束すると考えられます．

$$ \lim_{N_t(a) \to \infty} Q_t(a) = q_*(a)$$

ここで、N_t(a)は、時刻tまでに行動aがとられた回数を意味します

ε-greedy 法

では、探索と利用をバランス良く行うための最もベーシックな方法であるε-greedy 法について説明します． おさらいですが、greedyな行動選択とは常に最もよい選択のみを取り続けることを指します．つまり、探索を行いません．

ε-greedy 法では、基本的にはgreedyな行動をとり続け、たまにεの確率でランダムに行動選択を行います．

以下にε-greedy 法によるアルゴリズムを示します．

A simple bandit algorithm

Initialize,\; for\; a\; =\; 1\; to\; k:
\qquad Q(a) \leftarrow 0
\qquad N(a) \leftarrow 0

Repeat\; forever:
\qquad A\;\leftarrow \left\{ \begin{array}{} \underset {a} {\operatorname {argmax}} Q_t(a)\qquad with\; probobability\; 1-\varepsilon \qquad (breaking\; ties\; randomly) \\ a\; random\; action\; with\; probability\; \varepsilon \end{array} \right.
\qquad R\; \leftarrow bandit(A)
\qquad N(A)\; \leftarrow N(A) + 1
\qquad Q(A)\; \leftarrow Q(A) + \frac{1}{N(A)}[R - Q(A)]

実装例

ε-greedy法の効果を探るため、実際に学習を行ってみます．
実装にあたっては、githubで公開されているソースの一部を変更（無関係なところを削除）しています．

  • 問題設定 10本の腕を持つスロットを想定し、3000回の学習を行います．学習の目的は最良のアームを選択、得られる報酬を最大化することなります．学習は2000台のスロットに対して行い、獲得報酬、最良アーム選択率の平均を求めています．行動選択は、greedy法とε-greedy法の2つを行い結果の比較を行います．

  • 真の価値[tex:q*(a)]について 各アームの真の価値[tex:q(a)]は平均0、分散1の正規分布から決めています．また２平均[tex:q_(a)]、分散1の正規分布から、各アームを引いた際に得られる報酬を生成します．当然、q_*(a)の値や分布についてプレイヤーは知りません．

2000台のスロットそれぞれ、最良のアームおよび真の価値は異なることに注意してください．

  • 行動選択について アームの選択は、ε-greedy法を用いています．εの違いによる結果への影響を見るため、ε=0, 0.01, 0.1, 0.5, 1.0として比較しています．ε = 0 はgreedyな行動（利用）のみをとり、ε = 1 は探索ばかりを繰り返すことになります．

必要なライブラリのインポート

公開されているgithubのコードは、宣言をすれば改変が認められているんですね．絶対しませんけど． tqdmは、実行中のfor文に使うことでforループの進捗状況をバー表示することができます．

#######################################################################
# Copyright (C)                                                       #
# 2016-2018 Shangtong Zhang(zhangshangtong.cpp@gmail.com)             #
# 2016 Tian Jun(tianjun.cpp@gmail.com)                                #
# 2016 Artem Oboturov(oboturov@gmail.com)                             #
# 2016 Kenta Shimada(hyperkentakun@gmail.com)                         #
# Permission given to modify the code as long as you keep this        #
# declaration at the top                                              #
#######################################################################

import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import numpy as np
# 進捗状況を示すバーの表示
from tqdm import tqdm

Banditクラスの定義

ほぼ写経＋意味の追加です．元々のものはUCBアルゴリズムなどにも対応できるようしっかりと作りこまれていますが、今回の内容と関連しない部分は私の頭がついていけないので、削除しています．

少しはクラスの勉強しておいてよかった・・．

#Banditクラスの定義
class Bandit:
# @k_arm: # of arms
# @epsilon: probability for exploration in epsilon-greedy algorithm
# @initial: initial estimation for each action
# コンストラクタ
    def __init__(self, k_arm=10, epsilon=0., initial=0.,  true_reward=0.):      
        self.k = k_arm # 腕の数
        self.indices = np.arange(self.k) # k個のインデックスを作成
        self.time = 0 # time 初期値0
        self.average_reward = 0 # （平均）報酬の初期値0
        self.true_reward = true_reward # 真の報酬(クラス定義で指定しなければ0)
        self.epsilon = epsilon # クラス定義で指定しなければ0
        self.initial = initial # クラス定義で指定しなければ0
    
    # 初期化メソッド
    def reset(self):
        # real reward for each action
        # k本のアーム分、真の報酬を正規分布から選ぶ
        self.q_true = np.random.randn(self.k) + self.true_reward
        
        # estimation for each action
        # qの推定値の初期化（initialが0なら、0とするだけ）
        self.q_estimation = np.zeros(self.k) + self.initial

        # # of chosen times for each action
        # 行動選択の数の初期化→0に
        self.action_count = np.zeros(self.k)
        
        # ベストアクションの初期化→初期化したq_trueのうち、最大のもの
        self.best_action = np.argmax(self.q_true) 

    # get an action for this bandit
    # 行動（アーム）選択メソッド
    def act(self):
        #（乱数がεより小さければ完全にランダム）
        if np.random.rand() < self.epsilon:
            return np.random.choice(self.indices)
        # qの推定値の最大値をq_bestとする
        q_best = np.max(self.q_estimation)
        # q がq_bestと一致する行動の中からランダムで1つ選ぶ
        return np.random.choice([action for action, q in enumerate(self.q_estimation) if q == q_best])

    # take an action, update estimation for this action
    # 
    def step(self, action):
        # generate the reward under N(real reward, 1)
        # 報酬を平均（真の報酬）、分散１の正規分布からランダムに作成（スロットも確率的だということ）
        reward = np.random.randn() + self.q_true[action]
        
        self.time += 1
        
        # 平均報酬は、
        self.average_reward = (self.time - 1.0) / self.time * self.average_reward + reward / self.time
        
        # 行動カウンターを更新
        self.action_count[action] += 1
        
        #self.q_estimation[action] += 1.0 / self.action_count[action] * (reward - self.q_estimation[action])
        self.q_estimation[action] = (self.action_count[action] - 1.0) / self.action_count[action] * self.q_estimation[action] + reward / self.action_count[action]

        return reward

計算実行部分の定義

関数simulateで計算のメイン部分を行っています．

3つのfor文で構成されており、

  • 最初のfor文がインスタンスの数だけ回すループで、今回はパラスタを行うεの数である5回周ります．

  • 次のfor文が平均をとるために複数回同じ学習を回すループで、個のループは2000回まわります．

  • 最後のfor文が、1台に対して行う学習ステップで、今回は3000となります．

def simulate(runs, time, bandits):
  
    # ベストアクションカウンターと、報酬リストを空にする
    best_action_counts = np.zeros((len(bandits), runs, time))
    rewards = np.zeros(best_action_counts.shape)
    
    # インスタンスの数だけループ
    for i, bandit in enumerate(bandits):
      
        # 複数台のマシンに対するループ（平均をとるため）
        for r in tqdm(range(runs)):
            bandit.reset() # 初期化（マシンごとのベストアクション、価値はここで決められる）
            
            # 1台に対して行う学習STEP
            for t in range(time): #
                action = bandit.act() # 行動を選択
                reward = bandit.step(action) # 行動に対する報酬を取得
                rewards[i, r, t] = reward # 報酬リストに保存
                
                # 選んだ行動がベストアクションであれば、カウントする
                if action == bandit.best_action:
                    best_action_counts[i, r, t] = 1
                    
    # 学習曲線は、2000本(runの数だけ)存在する．
    # ベストアームを選んだ回数および報酬を2000台に対して平均を取る
    best_action_counts = best_action_counts.mean(axis=1)
    rewards = rewards.mean(axis=1)
    
    return best_action_counts, rewards

図化および計算実行用の関数

e_greedy()：インスタンスの定義を行い、実行用関数に渡しています．こんな風にリスト化したインスタンスを関数に渡せるんですね．

test_bed()：乱数で発生させた報酬の分布をviolinplotという方法で図化する関数．実際に学習の中で使っている乱数の値や分布とは異なりますが、概ねこういった分布をスロットの報酬として仮定しているということを示しています．という理解ですが間違っていたらご指摘ください．

f:id:shirakonotempura:20190124035035p:plain 
def test_bed():
# N(0,1)の標準正規分布からランダムに選んだ10の数値を平均μa．
# N（μa, 1)の正規分布からランダムに選んだ200の数値の分布を図化
# あくまでイメージ図のため200としているでOK？

    plt.violinplot(dataset=np.random.randn(200,10) + np.random.randn(10))
    plt.xlabel("Action")
    plt.ylabel("Reward distribution")
    plt.savefig('./images/test_bed.png')
    plt.close()

def e_greedy(runs=2000, time=3000):
    # epsilonのサイズでパラスタ（0はgreedy行動選択）
    epsilons = [0, 0.1, 0.01, 0.5, 1.0]
    # epsごとにインスタンスを作成、banditsにリストとして保存→次の関数へ
    bandits = [Bandit(epsilon=eps) for eps in epsilons]    
    best_action_counts, rewards = simulate(runs, time, bandits)

    plt.figure(figsize=(10, 20))

    plt.subplot(2, 1, 1)
    for eps, rewards in zip(epsilons, rewards):
        plt.plot(rewards, label='epsilon = %.02f' % (eps))
    plt.xlabel('steps')
    plt.ylabel('average reward')
    plt.legend()

    plt.subplot(2, 1, 2)
    for eps, counts in zip(epsilons, best_action_counts):
        plt.plot(counts, label='epsilon = %.02f' % (eps))
    plt.xlabel('steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('./images/e_greedy.png')
    plt.close()

if __name__ == '__main__':
    test_bed()
    e_greedy()

結果について

得られたグラフを以下に示します．

  • ε = 0.0 では常にグリーディな行動を選択します．そのため、 0.0以上の価値をもつ行動が見つかれば、その行動を常に選択し続けるようになり、それ以外の行動を探索しません．そのため，得られる報酬の平均値は常に一定（大体1.0程度）となっています．

  • ε = 0.01では、学習により報酬の平均値は1.5近くまで上がっています．3000 step以降でも、もう少し学習の余地がありそうです．学習のスピードは遅いですが、性能は最もよく学習ができているようです．

  • ε = 0.1,も、報酬の平均値は1.4程度に達しておりますが、必ず1割はランダム行動を行ってしまうため、報酬、最良アーム選択率とも頭打ちになっております．

  • ε = 0.5では、行動の半分をランダムに選択するため学習した結果を大分すてていることになります．平均では、greedy行動よりも悪い結果となってしまいました．

  • ε = 1.0では、学習した結果をまったく利用せずランダムな行動をとり続けます．そのため学習stepがいくら進んでも報酬の平均値や、最良アーム選択率はまったく上がっておりません．

f:id:shirakonotempura:20190124041145p:plain f:id:shirakonotempura:20190124041127p:plain

まとめ

強化学習の基本問題の１つであるバンディット問題について整理しました． ε-greedy法で、εが0.01や0.05が使われている理由が分かりました．

今回は行動（アーム）選択にε-greedy法のみを使用していますが、その他のアルゴリズムについてもまとめていきたいと思います．

今回の記事には、以下の記事を参考にさせていただきました

強化学習入門：多腕バンディット問題 - Qiita

バンディットアルゴリズム入門と実践