いきなりですが、状態価値関数・Bellman方程式について調べたくてこの記事にたどり着いた方は、何も考えずに以下の記事に飛んでください．時間を無駄にしなくてすみます．

今回から、上のQiitaに投稿された記事をトレースしながら状態価値関数からできればTD学習まで理解していきたいと思います．（絵はできるだけ自分で作成するようにしますが、描き方は参考にさせてください）

この記事は私の学習用ノートです．トレースです．元の記事は↑です．

今回の記事でまとめること

状態価値関数 $V^\pi(s)$ の導出
格子世界（Grid World）の状態価値関数の計算（Sutton本の3.5章）

特に後者は、本当にどうやって計算しているのかイメージできなかったので本当にありがたかったです．前者の導出もかなり丁寧に説明されています．

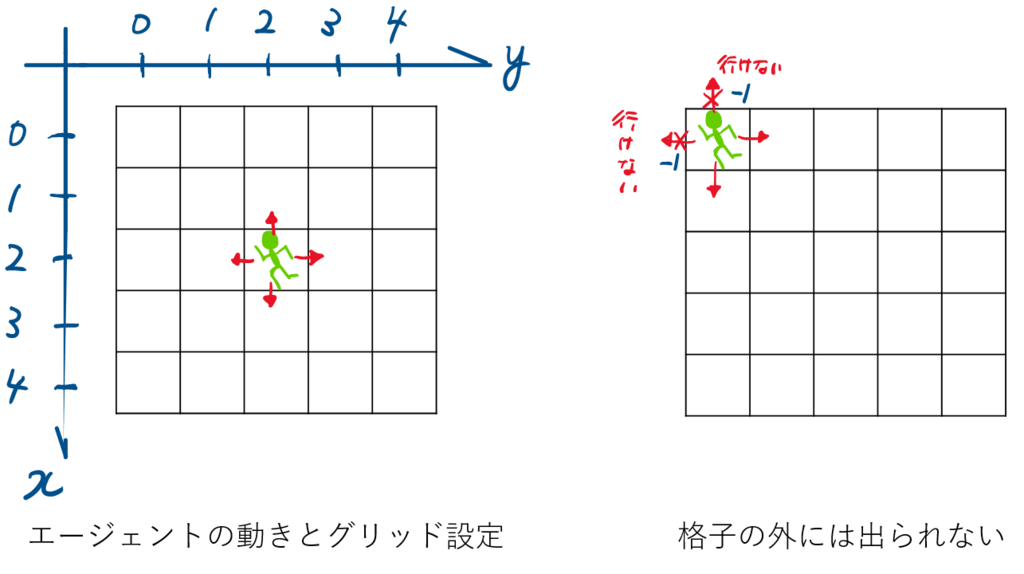
格子世界（Grid World）

今回の設定であるGrid Worldについて説明します．強化学習の例題で良く出てくるこの格子状のマス目の世界はGrid Worldと呼ばれています．

今回は5×5グリッドの世界を考えます．エージェントの上下左右に1マスずつ動きます（斜め方向は動きません）．

下図のように、x軸およびy軸は０から始まります．原点と正の向きについては、実際にGrid Worldを実装していく段階で重要になってきますので間違えないようにする必要があります．
エージェントはグリッドの外へ出ることはできません．出ようとする行動を選択することはありますが、その場合ペナルティとして負の報酬（-1）が与えられます．

f:id:shirakonotempura:20190126155117p:plain

図のAおよびBに到達した場合、その次の行動によらずAからはA'へ、BからはB'の状態に遷移します．その際、状態Aでとる行動には＋10の報酬が得られます．状態Bでとる行動には+5の報酬が与えられます．
恥ずかしながら、まずここの説明がテキストだけではよく理解できなかった．この説明のおかげでようやく問題の理解ができました．

f:id:shirakonotempura:20190126160041p:plain

その他、上記で明言していない行動に関しては、報酬は与えれません。（報酬０）

状態の価値

強化学習では、一般的にエージェントはあるポリシー $\pi$ に基づいて行動します．強化学習の目的は、長期的な収益を最大化するポリシーを求めることになります．

Grid Worldにおけるエージェントの場合だと

できるだけ上を多く選ぶ
右に動いた後は、下を選ばないなどがポリシーになります．

ということは、ご飯を食べた後すぐは運動しない、というのも人間のポリシーの１つですね．

話がそれましたが、状態の価値に話を戻します．今回のGrid Worldにおいてどの状態（グリッド）の価値が高いでしょうか．報酬がもらえるマスAやBの価値は間違いなく高そうです．となると、AやBに近いマスの価値も高くなりそうです．一方で、壁際のマスは、負の報酬を得る可能性があるので低くなってしまいそう．特に下側の方は、AやBからも遠いので価値は低そうな気がします．

それらの価値を求めるのが今回の目的になります．Sutton本ではいきなり価値関数が計算されているんですが、ちょっとはしょりすぎだと思いました．

このとき、状態の価値はポリシーによって変わるということに注意してください．例えば、オレは絶対右には動かない！というポリシーをエージェントが持っていたとすると、マスAの左にいることの価値は低くなります．

ポリシー（方策、戦略）の定式化

まず、ここでポリシーについて定式化をしておきます．

ポリシーは、ある状態sの時に行動aを取る確率として定義することができます．

Grid World上のある状態（ｘ=2, y = 3）において、右に0.7、その他に0.1ずつの確率で移動するという方策は

$$ \pi(s, a) = \left\{ \begin{array}{} 0.7 \qquad(s = (2, 3), a = right) \\ 0.1 \qquad(s = (2, 3), a = up) \\ 0.1 \qquad(s = (2, 3), a = left) \\ 0.1 \qquad(s = (2, 3), a = down) \end{array} \right.$$

となります．それぞれの状態sについて行動aそれぞれの確率を返すわけですから、全ての方策を配列に格納しようとすると、状態25×行動4＝100個の値が必要となります．これを

$s\in S, a\in A, \pi \in S × A$ と表したりします．

実際にポリシーの学習を行う場合には、各状態におけるポリシーを状態によらず同じ確率分布をとると設定することもよく行われます．

今回はこのポリシーの学習は行いません．というか、しばらく行いません．

今回のエージェントのポリシー： 『上下左右の行動はランダムに等確率で選択する』です

元記事でも書かれていますが、決まった方策のもとでの状態価値関数を導出するのが目的となります．

価値の定式化

ポリシーが定式化できましたので、いよいよ状態価値を定式化していきます．そのため、価値関数（Value Function）という概念を導入します．

価値関数は以下の2種類があります．

状態価値関数（State Value Function)　 $V^\pi(s)$
- 状態s（にいることの）価値．
行動価値関数（State Value Function)　 $Q^\pi(s,a)$
- 状態sにいて行動aを取ることの価値． $Q^\pi(s,a)$ は行動に対して求められので、仮に今回の問題で求めるとすると1マスに対して4つのQ値が求まることになります．

今回は、状態価値関数 $V^\pi(s)$ を求めます．

では、情報価値の定式化にあたり、前回使用した強化学習のシステムを再度確認します．

f:id:shirakonotempura:20190126033017p:plain

時刻t（図の左端）に状態 $S_t$ にいたとき、ポリシー $\pi$ に従って行動 $A_t$ を取った結果、時刻t+1で状態 $S_{t+1}$ に遷移し、報酬 $R_{t+1}$ を受け取ります（このときの報酬は $R_{t+1}$ であることに注意してください）．これを時々刻々繰り返していきます．

ここで、時刻tにおける状態 $S_t$ の状態価値 $V^\pi (S_t)$ を

『状態 $S_t$ を起点に、ポリシー $\pi$ に従って行動をとり続けた時の報酬の合計（つまり、収益）』

と定義してみます．

『とり続けた』と定義したように、終わりがくるまで永遠に行動をとり続けます．今回のGrid Worldの問題では終了条件はセットしていませんので、状態価値 $V^\pi (S_t)$ を求めるために、永遠に報酬を足し続けることになってしまいます．

当然、それでは計算が収束しませんので、前回登場した時間が経過するにつれて報酬を割り引く割引係数 $\gamma$ を使います． $0 \leq \gamma \leq 1$ なので遠い未来ほど値が小さくなります． $\gamma$ の大きさにより、未来をどれだけ重視するかを調整することができます．

f:id:shirakonotempura:20190126162521p:plain

上の図と同じように、時刻t+1を起点として、 $V^\pi (S_{t+1})$ についても考えてみましょう．１つ右にずれるだけですので、難しくないはずです．

f:id:shirakonotempura:20190126162543p:plain

では、再度時刻tにおける $V^\pi (S_t)$ を考えます．時刻t+1以降の報酬は $V^\pi (S_{t+1})$ に集約されていますので、 $V^\pi (S_{t+1})$ を使えば以下のように $V^\pi (S_t)$ が書けるような気がします．

$$V^\pi (S_t) = r_{t+1} + \gamma V^\pi (S_{t+1})$$

かなり、すっきりとした式になりました．ある時刻における価値関数は、その先の時刻における価値関数の漸化式になっているようです．

しかし、厳密にはこの式は成立しません．価値関数が持つ性質の見落としがあるためです．以下で詳しく見ていきます．

正しい価値関数の導出

方策による枝分かれ

先に示したダイアグラムでは２つの見落としがありました．1つ目は

ある状態 $s$ からポリシー $\pi$ に従ってとる行動 $a$ は一義的には決まらない

ということです．ポリシーの説明で、ある状態での行動は確率的に決められると書いたように、他の行動が選ばれる可能性もあったということになります．当然、実際に選択して行動にうつすのは1つだけなのですが、行動を決める際には他の行動が取られる可能性が存在し、それが選択されたと場合の未来も存在していたということになり、以下のように枝分かれした未来を考慮する必要があります．

f:id:shirakonotempura:20190126165038p:plain

遷移確率による枝分かれ

さらに見落としている分岐がもう１つあります．それは

状態 $s$ でポリシー $\pi$ に従って行動 $a$ が選ばれたとき、それに対応する状態 $s'$ は一義的には決まらない

ということです．エージェントがはれて右に行くという選択をしたのに、右に行くとは限らないなんて・・・．ですが、これも遷移確率（Transition Probability）というちゃんとした名前が付けられています．ポリシーの確率分布と混同しそうになりますが、例えば95%の確率で指示通りに動作するけど、たまに想定外の動作をするロボットなんかがイメージしやすいかもしれません。

任意の状態 $s$ と行動 $a$ が与えられた場合の、次に可能な各状態 $s'$ の確率は

$$P^a_{ss'} = P_r [s_{t+1} = s' | s_t = s, a_t = a]$$

と表されます．またその際の報酬は $R^a_{ss'}$ と表します．方策による枝分かれにさらに遷移確率による枝分かれを考慮したダイアグラムは以下のようになります．

f:id:shirakonotempura:20190126165021p:plain

なんかめちゃくちゃ複雑になってしまいましたが、ようやく状態価値関数を正しく表す準備が整いました．

状態価値関数の導出とBellman方程式

あらためて、先ほど定義した状態価値関数の式を示します．

$$V^\pi (S_t) = r_{t+1} + \gamma V^\pi (S_{t+1})$$

こちらに見落としていた２つの枝分かれの影響を考慮していきます．

方策と遷移確率を考慮するためには、さきほどダイアグラムで示したようにとりうる分岐の全てを考慮して報酬を合計する必要があります．どのようにするかというと、それぞれの枝の重みに枝分かれがとる確率をあてはめていきます．つまり期待値を計算することになります．

上記を考慮して、状態価値関数の定式化を行うと以下のようになります．

$$V^\pi (s) = \sum_{a} \pi(s,a) \sum_{s'}P^a_{ss'} [R^a_{ss'} + \gamma V^\pi (s')]$$

この式を、日本語で訳してみると
状態価値関数は、直近の報酬に1ステップ先の状態価値関数を足したものである．ただし、方策および遷移確率で未来のとりうる値は枝分かれするので、その期待値をとる

このような漸化式を状態価値関数 $V^\pi$ に対するBellman方程式と呼びます．

数式

最後に、Sutton本で書かれている状態価値関数の導出を載せておきます．元の記事でも書かれているように、この式を覚える必要はないかと思います．

$$\begin{eqnarray} V^\pi (s) &=& E_\pi [R_t|s_t = s] \\ &=& E_\pi \biggl[\sum_{k=0}^\infty \gamma^k r_{t+k+1}|s_t = s\biggr] \\ &=& E_\pi \biggl[r_{t+1} + \gamma \sum_{k=0}^\infty \gamma^k r_{t+k+2} | s_t = s\biggr] \\ &=& \sum_{a} \pi(s, a) \sum_{s'} P^a_{ss'} \biggl( R^a_{ss'} + \gamma E_\pi \biggl[ \sum_{k=0}^\infty \gamma^k r_{t+ k + 2} | s_{t+1} = s' \biggr] \biggr) \\ &=& \sum_{a} \pi(s,a) \sum_{s'}P^a_{ss'} [R^a_{ss'} + \gamma V^\pi (s')] \\ \end{eqnarray}$$