はじめに

前回は、近似式と目標値の差を表す誤差関数を最小化するパラメータの探索手法の１つである勾配法について整理しました．

今回は、強化学習におけるパラメータの更新について詳しく見ていきます．

この記事は私の学習用ノートです

パラメータ $\boldsymbol{w}$ の更新

以下では、Sutton本に合わせて状態価値関数 $V(s)$ を使って説明しています．もちろん、行動価値関数 $Q(s,a)$ にも関数近似は適用できます．行動価値関数のパラメータ更新については最後に紹介するようにします．

誤差関数（おさらい）

『真の状態価値 $v^* (s)$ 』と『近似式による推定値 $\hat{v}(s,\boldsymbol{w})$ 』を使った誤差関数 $E_{SE}(\boldsymbol{w})$ をあらためて示します．これは、教師あり学習のやり方に沿って定式化したものになります．

$$E_{SE}(\boldsymbol{w}) = \sum_{s}[v^* (s)- \hat{v}(s,\boldsymbol{w})]^2 \qquad \cdots (1)$$

この誤差関数を最小化するパラメータ $\boldsymbol{w}$ を勾配法を使って求めたいのですが、式中 $v^* (s)$ で示した真の価値（教師あり学習で言う正解データ）は、強化学習では与えられません．

そのため、何か真の価値の代わりになるものをターゲットにする必要があるのですが、とりあえずそのままターゲット（ $Target$ ）と呼ぶことにします．

ターゲットは自分で行動して決める

具体的なターゲットの中身は後程説明しますが、どのようにターゲットを決めるかと言うと、強化学習ではこれまでと同じように行動しながら決めることになります．

教師あり学習をベースにした(1)式では複数の正解データが与えらることを想定して誤差の２乗和（ $\sum$ ）を取っていましたが、強化学習における誤差関数は、ターゲットと近似値の差の２乗を毎ステップ、誤差関数として計算することになります．

以上のことから、強化学習における誤差関数は以下の(2)式のように表します．ややこしいので添え字のSEは消しました．

$$E(\boldsymbol{w}) = [Target- \hat{v}(s,\boldsymbol{w})]^2 \qquad \cdots (2)$$

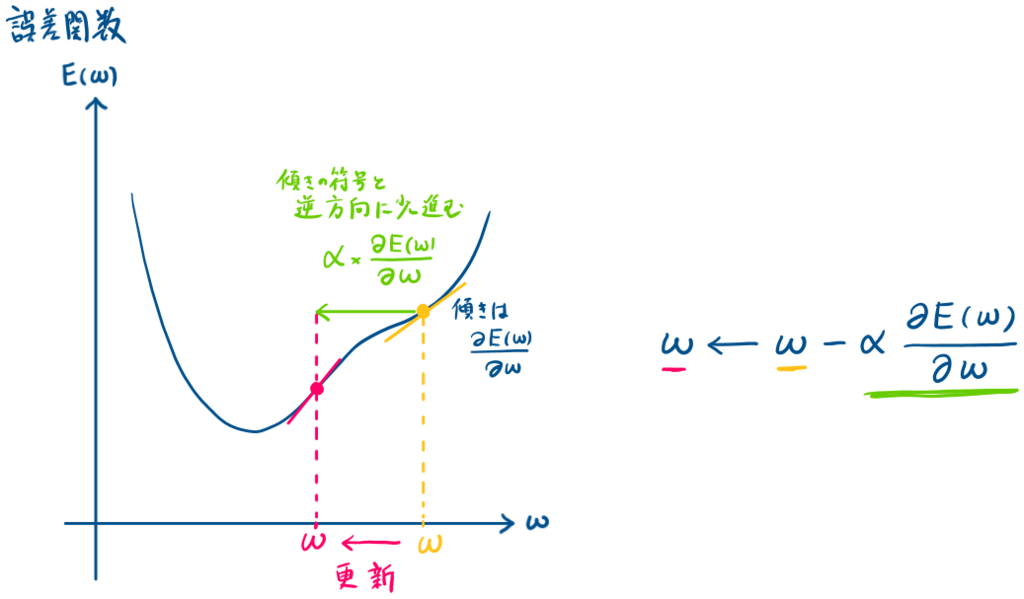
図におけるイメージで説明

では、(2)式を最小化するパラメータ $\boldsymbol{w}$ を求めることになりますが、以下に誤差関数 $E(\boldsymbol{w})$ の更新イメージを示します．

f:id:shirakonotempura:20190216093600p:plain

式の導出

正直、導出と呼べるほどのことはしていませんが語彙力不足のため、他の言葉が思い浮かびませんでした．
要は、上のイメージを式で表していくだけです．

上に示したイメージ図から、更新されるパラメータ $E(\boldsymbol{w})$ は(2)式で表すことができます．(3)式中の $\alpha$ は学習率（定数）になります．

$$ \boldsymbol{w}\leftarrow \boldsymbol{w} - \alpha \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}} \qquad \cdots (3)$$

(3)式中の、 $\frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}$ の部分は(2)式で示した誤差関数 $E(\boldsymbol{w})$ のパラメータ $\boldsymbol{w}$ による偏微分を示すので、(2)式を使うと以下のように書くことができ、(4)式が得られます．

$$\begin{eqnarray} \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}} &=& \frac{\partial}{\partial \boldsymbol{w}} \Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr]^2 \\ &=& 2\Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr] \Bigl(- \nabla \hat{v}(s; \boldsymbol{w})\Bigr)\\ &=& -2\Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr] \nabla \hat{v}(s; \boldsymbol{w}) \qquad \cdots (4)\\ \end{eqnarray}$$

(4)式を(3)式に代入すると、以下のように書けます．

$$ \boldsymbol{w} \leftarrow \boldsymbol{w} + 2 \alpha \Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr] \nabla \hat{v}(s; \boldsymbol{w}) $$

これで、大方の形は出来上がりましたが、少しだけSutton本に合わせて化粧をします．

まず、 $2\alpha$ は定数になりますので、まとめて $\alpha$ としてしまいます．また時刻 $t$ における状態 $s_{t}$ におけるパラメータ $\boldsymbol{w}_{t}$ の更新という意味で添え字を付けます．

$$ \boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[Target - \hat{v}(s_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{v}(s_t; \boldsymbol{w}_t) \qquad \cdots (5)$$

これで、パラメータ $\boldsymbol{w}$ の更新式の基本の形は完成になります．

Targetについて

いよいよ問題のターゲット（Target）について、説明していきます．

基本的には、これまでのテーブル形式でやってきた更新と考え方は同じです．テーブル型における、TD(0)学習の更新式を以下に示します．（sutton本の(6.2)式）

$$ V(s_t) \leftarrow V(s_t) - \alpha [R_{t+1} + \gamma V(s_{t+1}) - V(s_t)]$$

上記の式における $R_{t+1} + \gamma V(s_{t+1})$ は、報酬 $R_{t+1}$ と遷移後の状態価値 $V(s_{t+1})$ を使った、『状態 $s$ における状態価値 $V(s_t)$ の推定値』になります．学習率を使っているのでいきなり置換するわけではありませんが、これが目標値になっていました．

関数近似においても、同じくこの推定値を目標値と考えることができます．
テーブル型の場合は、 $V(s_{t+1})$ の部分をテーブルを用いて求めていましたが、今回はそこが近似式を使った近似値になるだけです．

つまり、 $V(s_{t+1})$ を $\hat{v}_(s_{t+1}:\boldsymbol{w})$ に置き換えればよく、関数近似における目標値は以下のように表すことができます．

$$R_{t+1} + \gamma \hat{v}_(s_{t+1}:\boldsymbol{w})$$

これを(5)式の $Target$ に代入すれば以下の(6)式が得られます．

$$ \boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[R_{t+1} + \gamma \hat{v}_(s_{t+1}:\boldsymbol{w}) - \hat{v}(s_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{v}(s_t; \boldsymbol{w}_t) \qquad \cdots (6)$$

疑似コード

最後に疑似コードを示します．

f:id:shirakonotempura:20190220024925p:plain

出典：R.Sutton and G Barto, Reinforcement Learning An Introduction, pp.203

行動価値関数への適用（10章、On-Policy Controlの範囲）

ここまで、状態価値関数 $V(s)$ を中心に説明してきましたが、当然、行動価値関数 $Q(s,a)$ も $\boldsymbol{w}$ をパラメータに持つ関数を用いて近似することができます．

行動価値関数では状態 $s$ と行動 $a$ を入力になりますので、(6)式をもとにした行動価値関数のパラメータ更新式は以下のように書くことができます．（Sutton本の10章、(10.2)式に該当します）

$$ \boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[R_{t+1} + \gamma \hat{q}_(s_{t+1}, a_{t+1}:\boldsymbol{w}) - \hat{q}(s_t, a_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{q}(s_t, a_t; \boldsymbol{w}_t) \qquad \cdots (7)$$

局所最適解について補足

前回、最適化において局所解に落ち込んでしまうことを問題に挙げました．
しかし、Sutton本の9.2章をよく読んでみると

『理想としては、すべてのパラメータ $\boldsymbol{w}$ に対して誤差関数が最小となる $\bar{VE} ( \boldsymbol{w}^{*} ) \leq \bar{VE}( \boldsymbol{w} )$ となる $\boldsymbol{w}$ * を求めることである．しかし、（中略）それが求まる可能性はほとんどない．』