f:id:shirakonotempura:20190213075046j:plain

追記（謝罪）：偏微分の式で分母にしか記号 $\partial$ を付けていませんが、正しくは分子にも必要なようです．以後気を付けます．

はじめに

前回に続き、関数近似について整理していきます．前回は途中で疲れ果ててしまいました・・．

強化学習：関数近似（その１：導入） - 他力本願で生き抜く（本気）

今回は、主にパラメータを更新する際に用いる勾配降下法についての内容となります．これはかなり教師あり学習の内容とかぶりますが、あまり理解してこずに放置していた内容になりますので、いい機会なので整理しておきます．

教師あり学習との類似点と違い

前回説明した基底関数が決まれば、いよいよ近似関数のパラメータ調整に入っていきます．

教師あり学習では、推測値と正解（教師）データの差の2乗和、つまり２乗誤差が小さくなるようにパラメータを更新しました．

強化学習において、推測値に相当するのが近似関数によって出力される価値関数、正解データに相当するものが真の価値関数になります．

つまり、強化学習においては、『真の価値』と『近似関数による推定価値』の２乗誤差を最小化するためにパラメータ $\boldsymbol{w}$ の更新を行っていきます．この枠組みは教師あり学習と同じ考え方です．

f:id:shirakonotempura:20190213081922p:plain

しかし、教師あり学習と決定的に違う点は強化学習においては、当然、真の価値関数は与えられないという点です．そのため、真の価値関数に代わるものを考えなければならないのですが、とりあえずは真の価値関数という表現を使って話をすすめます．

先に言っておくと、真の価値関数の代わりになるものを試行を通じて求め、それを正解データのように扱うということで学習は進んでいきます．この辺は、次回以降もう少し詳しく説明する予定です．

f:id:shirakonotempura:20190213082748p:plain

二乗誤差の計算

話を簡単にするため、以降では状態価値関数に話を限定して

真の価値関数を $v^*(s)$
関数近似による推定価値関数を $\hat{v}(s, \boldsymbol{w})$

とします．

この記号を使えば、２乗誤差（Squared Error）は以下のように定義できます．

$$E_{SE}(\boldsymbol{w}) = \sum_{s}[v^* (s)- \hat{v}(s,\boldsymbol{w})]^2$$

教師あり学習であれば、次に $E_{SE}$ の勾配を求めるため、 $E_{SE}$ をパラメータ $\boldsymbol{w}$ で微分してという流れになるのですが、ここは一旦これで止めておきます．

◇◇ 悩み中（On Policy Distributionについて) ◇◇

Sutton本9.2章に以下の式が(9.1)式として出てきます．

$$\bar{VE}(\boldsymbol{w}) \dot{=} \sum_{s \in S} \mu(s) [v_\pi(s) - \hat{v}(s,\boldsymbol{w})]^2$$

右辺は各状態 $s$ における二乗誤差の総和を表しているのですが、右辺の $\mu(s)$ がどうしても理解できません．on-policy distribution と呼ぶみたいですが、ある状態 $s$ の重みでしょうか？引き続き理解に向けて勉強しますが、万が一、詳しい方が見ていれば教えてください・・．

関数近似と勾配法

さて、強化学習におけるパラメータ $\boldsymbol{w}$ の更新に関する内容は次回以降に回すことにしましたので、ここでは近似を行う方法に関して、もう少し一般的な話をしたいと思います．
先に書いたように、近似にはターゲットが必要となりますので、ここではターゲットとして、正解データが与えられた教師あり学習を例に挙げて説明します．

例題

f:id:shirakonotempura:20190214010046p:plain

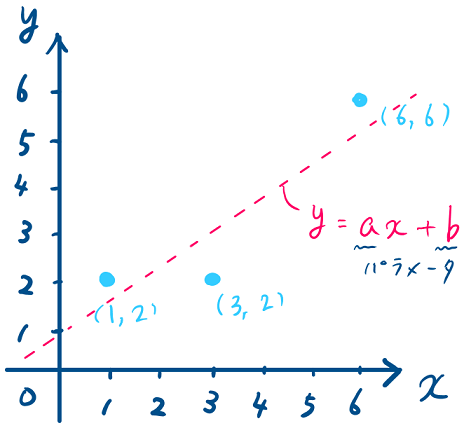
上記に示した水色の３点を $y = ax + b$ の１次式で近似することを考えます．この場合、求めたいパラメータは $a$ および $b$ の２つになります．

手計算でやってみる

最初に手計算でパラメータを求めてみたいと思います．

手計算であろうと勾配法であろうと、最初にやることは誤差関数を求めることになります．

f:id:shirakonotempura:20190214013731p:plain

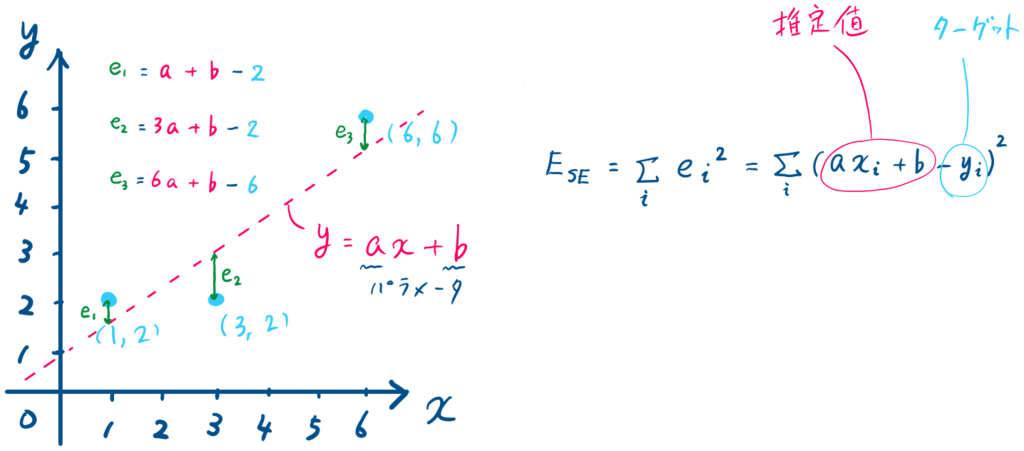
$a,b$ をパラメータとする誤差関数 $E_{SE}(a, b)$ はターゲットと推定値の差（図中の $e_{i}$ )の総和となり、式を展開すると以下のようになります．

$E_{SE}(a,b) = 46a^2 + 3b^2 + 20ab - 88a -20b +44\qquad \cdots (1)$

この誤差関数が最小となるようにパラメータ $a,b$ を求めます．
$E_{SE}(a,b)$ が最小となるのは、(1)式を $a,b$ でそれぞれ偏微分した $\frac{E(a,b)}{\partial a}$ 、 $\frac{E(a,b)}{\partial b}$ が０となるとき（※1）なので、以下の連立方程式を解くことでパラメータ $a,b$ を計算することができます．

$\frac{E(a,b)}{\partial a} = 92a + 20b - 88 = 0$
$\frac{E(a,b)}{\partial b} = 20a + 6b -20 = 0$

（もうちょいましな係数にすべきだったと後悔）

これを解くと、 $a \fallingdotseq 0.842$ 、 $b \fallingdotseq 0.526$ が得られます．

※1：
誤差関数 $E(a,b)$ を $a$ で偏微分する場合、パラメータ $b$ は定数扱いになり、 $E(a,b)$ は下に凸の２次関数 $E(a)$ とみなせます．そのため、微分して得られる傾きが０となる点は関数 $E(a)$ の谷底となり、その点は $E(a)$ を最小化する $a$ になります．同様にして、関数 $E(b)$ を最小にするパラメータ $b$ も計算することができます．

f:id:shirakonotempura:20190214023244p:plain

（この絵はイメージのため、都合よく書いています．誤差関数は極値（谷とか山になる頂点）が複数あることがほとんどです）

勾配法でやってみる

次に、勾配法（Gradient Method）を使ってパラメータを求めてみます．

勾配法は最適化手法の一つで、あるパラメータを持つ評価関数が最小や最大になるときのパラメータを求めることができます．上の例題は、問題設定が簡単なので手計算で解けてしまいましたが、関数の表現力をあげると、パラメータの数も増えることになりますので、一般的に手計算では手に負えません．

まずは、おそらく一番ベーシックな最急降下法と呼ばれる手法について紹介し、次にそれにランダム性を加えた確率的勾配降下法を紹介したいと思います.

◇◇ 補足（雑談）◇◇

パラメータ $\boldsymbol{w}$ や $\boldsymbol{\theta}$ の更新に使う勾配降下法ですが、勾配降下法と最急降下法といいう言葉が混同されていることがあります．

個人的には、勾配降下法（または勾配法、Gradient Method）の具体的な方法の１つが最急降下法（Gradient Descent）であったり、次に説明する確率的勾配降下法（Stochastic Gradient Descent）となるという理解です．たぶんこれはあっているはずです．
ただ、確率的勾配降下法はランダムにピックしたサンプルに対して最急降下法の適用を繰り返すことだと思うので、確率的最急降下法と呼ぶべきなんじゃないかと思っています．とはいえ、なじみのない言葉を使っても仕方ありませんので、SGDは確率的勾配降下法として説明していきます．

この記事では、勾配降下法は傾きを使ってパラメータの更新を行う方法全般のことを指し、最急降下法（GD）、確率的勾配降下法（SGD）は具体的な手法の１つを指すものとします。

最急降下法（Gradient Method）

最急降下法は、ざっくり言ってしまえば、傾きと逆の方向にちょっとだけ進むことを繰り返す方法です．アルゴリズムは非常にシンプルです．

最小化したい誤差関数 $E_{SE}(a,b)$ は先ほど式(1)で示したものですが、パラメータ $a,b$ をまとめてベクトル $\boldsymbol{w} = (a, b)^T$ を使って表すことにします．

誤差関数 $E_{SE}$ を $\boldsymbol{w}$ で偏微分する
- 要は、 $E_{SE}$ を $a$ および $b$ で偏微分することなので、手計算のときに出てきた連立方程式のことです．
適当にパラメータ $\boldsymbol{w}$ を決める
- 適当に $a$ および $b$ を選びます．これがパラメータの初期値になります．
現在のパラメータを使って誤差関数 $\boldsymbol{w}$ の傾き $\frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}$ （=勾配ベクトル）を求める
- 具体的には、1.の連立方程式に2.で決めた $a$ と $b$ を代入します．
- つまり現在の位置における勾配を求めていることになります．
最急降下方向に進む（勾配ベクトルの符号と逆方向）
- ここが先に書いた、逆方向にちょっとだけ進むに相当します．
- 3.で計算した勾配ベクトルに沿って、最も小さくなる方向（最急降下方向）に動きたいのですが、その方向は勾配ベクトルと符号が逆になります．
- よって、以下の式でパラメータ $\boldsymbol{w}$ を更新します．（式中の $\alpha$ は学習率で0.01や0.05のような値が使われます．） $$\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}$$
- 今回の例で、もう少し具体的に書くと $$a \leftarrow a - \alpha \frac{\partial E(\boldsymbol{w})}{\partial a}$$ $$b \leftarrow b - \alpha \frac{\partial E(\boldsymbol{w})}{\partial b}$$
$\boldsymbol{w}$ が収束するまで、上記3と4を繰り返す

f:id:shirakonotempura:20190214064120p:plain

ちょっと図がごちゃごちゃしてますが、右図は左の図の一部を拡大したと思ってください．

このように最急降下法では反復計算によって、パラメータの推定を行います．
そのため先の例を最急降下法で解こうとすると、この紙面では足りないので一部省略しますが、次のような計算を繰り返すことになります（学習率 $\alpha=0.01$ としています）．

$E(\boldsymbol{w})/\partial a = 92a + 20b - 88$
$E(\boldsymbol{w})/\partial a = 20a + 6b - 20$

t=0
$a = 0$ , $b = 0$
$E(\boldsymbol{w})/ \partial a = 92 * 0 + 20 * 0 - 88 = - 88$
$E(\boldsymbol{w})/ \partial b = 20 * 0 + 6 * 0 - 20 = - 20$
$a \leftarrow 0 - 0.01 * (-88) = 0.88$
$b \leftarrow 0 - 0.01 * (-20) = 0.20$
t=1
$a = -0.88$ , $b = -0.20$
$E(\boldsymbol{w}/\partial a = 92 * 0.88 + 20 * 0.20 - 88 = - 3.04$
$E(\boldsymbol{w}/\partial b = 20 * 0.88 + 6 * 0.20 - 20 = - 1.2$
$a \leftarrow 0 - 0.01 * (-3.04) = 0.9104$
$b \leftarrow 0 - 0.01 * (-1.2) = 0.212$
：

こんな感じで、反復計算を続けていけば３５０ステップくらいで $a = 0.842$ 、 $b = 0.526$ に収束します．

確率的勾配降下法（Stochastic Gradient Method）

では、次に確率的勾配降下法について説明します．これは英語の頭文字を取ってSGDと呼ばれたりします．こっちはさらっと行きます．

この方法は、簡単に言えば、最急降下法にランダム性を持たせたものになります．

これまでの説明において誤差関数 $E(\boldsymbol{w})$ は、ターゲットと推定値の誤差の総和としてきました．つまり、誤差関数 $E(\boldsymbol{w})$ を計算するためには全てのデータが必要でした．
それに対し、SDGでは誤差関数の計算にはサンプルデータ１つを使います．ただし、どれをサンプルに使うかは各反復でランダムに選びます．

サンプルデータを１つしか使わないということは、なかなか収束しないような気がするのですがこれでうまくいくようです．サンプルが３つしかない今回の例題は例外でした．

では、なぜランダムに選ぶのかを理解するには、最急勾配法の問題点を考える必要があります．最急降下法では、適当に選んだ初期パラメータから、ちょっとずつパラメータの更新を行いました．しかし、もし下図のような誤差関数があった場合、初期パラメータの選び方によっては、誤った解に収束してしまいます．

f:id:shirakonotempura:20190214092749p:plain

一方、SDGは、初期値に依存せずに最適パラメータを探すことになりますので、局所解に落ち込むリスクは最急降下法よりは小さいと言えます．

一般的にSDGは最急降下法より優れているみたいなので、SDGを使えば問題ないんだろうとは思いますが、一応以下にメリット・デメリットを上げておきます．

メリット
- 一方向から探す解を探すわけではないので、局所解に落ち込みにくい
- 全データを必要としないので、データを取りながらのオンライン学習に使える
- 計算が早い（らしい．これは実感していないのでわかりませんが、収斂回数は増えるけど、一回の計算に使うデータが１つなので、結果的に早くなるようです）．
デメリット
- ランダム性を含むので、最短では解にたどり着かない．
- 異常値があった場合、それに引っ張られやすい．（データを見てなんとかしましょう）

なお、最急降下法とSDGを組み合わせた、ミニバッチ勾配降下法（Mini Batch Gradient Descent）という方法が考えられています．これは最急降下法のように全データを使うわけではなく、いくつかのデータを選んで誤差関数を求める方法になります．