強化学習:関数近似(その1:導入)
はじめに
今回から、Sutton本9章の内容について勉強しながら、関数近似についてまとめていきたいと思います.Sutton本では、この章(9章)からは第2部となっており、これまでTabular(表形式)で扱っていた状態を関数近似によって拡張していく内容になります.
これまでの場合、『状態、行動』が与えられたら、それに対応する『報酬、次の状態』をTableから選んで返すということができたわけですが、格子世界のような限られた状態に落とし込める問題というのは、現実にはそこまで多くありません。仮にあったとしてもその状態数が多かった場合、すべてを表形式で扱うことには限界がありそうなことは何となくイメージできるかと思います.
そこで状態評価や戦略をパラメータを持った関数で近似的に表してしまうことで、表では表現できなかった連続的な状態を表現することが可能になってきます.また、この関数近似によって強化学習とニューラルネットが結びつき深層強化学習(Deep Reinforcement Learning)に繋がっていくことになります.
ニューラルネットワークの説明に関しては、ここでは行いませんので以下の記事を参考にされてください. Chainerで始めるニューラルネットワーク - Qiita
【入門向け】ニューラルネットワークの仕組みを緩く図解 - Qiita
価値関数の近似
では、価値関数を近似するということを具体的にみていきます.
これまで価値関数は、状態価値や行動価値
という表現をしてきました.
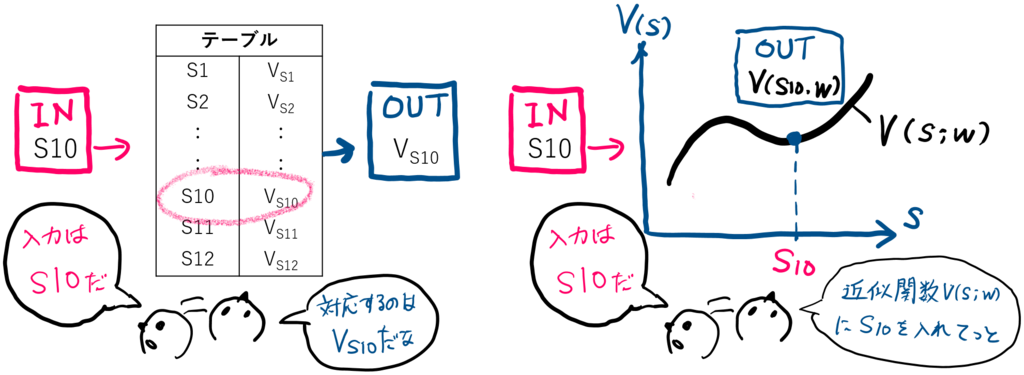
くどいですが、関数近似のイメージを掴むため2×2の格子世界を考え、それぞれの状態価値を下記左図のように仮定します.ここでは、状態価値の関数近似をイメージしてます.
これを横軸に状態、縦軸に状態価値
として無理やりグラフに落とし込みます(下図中央).
この状態と状態価値
の関係性をパラメータ
を使って関数にしてしまうことで、テーブル表現だった価値関数を(近似)関数で表してしまおうというのが関数近似となります.先にも書いたように、このような関数の形で表現することで、離散的(とびとび)にしか扱えなかった状態や状態価値を、連続値として評価することが可能になります.

関数近似(Function Approximation)の種類
上のイメージ図は、状態を入力として状態価値
を推定する近似関数を例として表しましたが、関数近似は入力と出力の対象によって大きく3種類に分けることができます.
- 状態
を入力にして、状態価値を関数
で表す
- 状態
と行動
を入力にして、行動価値を関数
で表す
- 状態
を入力にして、行動
の数だけ行動価値を関数
で表す.

関数近似に用いる関数について
近似関数はパラメータを使って関数
や
のように表すと書きましたが、実際は近似のベースになる関数は決めてあげる必要があります.このベースとなる関数は基底関数と呼ばれ、
で表されます.
基底関数の決め方にはルールはありませんので、基本的にどんな関数を使ってもいいのですが、以下に代表的なものを2つ紹介しておきます.
- 多項式基底: $$\phi_i (x) = x^i (i=0, 1, \cdots,M - 1) $$ 多項式基底では関数を多項式で表すことになります.
- ガウス基底:
$$\phi _i (x) = exp\biggl[-\frac{(x - \mu_{i})^2}{2s ^2}\biggr] (i=1, \cdots,M) $$
ガウス基底は、平均および標準偏差
を選んで定義します.正規分布と同じ釣り鐘状の関数を表現します.
近似関数はパラメータを調整しさえすれば、あらゆる形状が表現できる関数が望ましいのですが、1つの基底関数での表現力はその式の形状でしかありません.そのため、実際は基底関数を複数組み合わせることで、近似関数の表現力を高めてやる必要があります.
以下に、ガウス基底を使った近似関数の例を示します.左図が1つのガウス基底によるもので、右図が9つのガウス基底を使ったものになります.左図がガウス基底(正規分布)の形状しか表せていないのに対して、右図の関数はかなりの表現力を持っていそうなことがイメージできるかと思います.(この例では、パラメータによって各山の高さが変わります.)

まとめ
内容に収集がつかなくなってきましたので、一旦終わります.
- 関数近似の概要を整理しました.
関数近似に関しては、もう2回くらいかけて
- 勾配降下法について内容
- パラメータの更新
などについて整理したいと思います.