2022-04-21

androdスマホからiPhoneへ電話帳（連絡先）を移行する方法

android iPhone 電話帳

これまで、電話専用スマホ(android）とデータ専用スマホ（iPhone）の2台持ちをしていたのですが、さすがに2台持ちがしんどくなってきましたので、iPhoneに統合することにいたしました。

結果的に移行は無事できましたが、ほんの少しですが、トラブったので備忘メモです。

状況：

電話専用スマホはへは、ドコモショップでガラケーから電話帳移行をしてもらっていました。
移行元はandroid arrows F-41A、以降先はiPhone13

標準的な方法は以下の方がまとめれくれておりますので、大半の方はこちらの対応で済むと思います。

mobareco.jp

①「Googleアカウント」を使って移行する

②「JSバックアップ」アプリを使って移行する

③「microSDカード」と「パソコン」を使って移行する

私もwifiの環境がありましたので、まずは①の方法を試してみました。

症状１：一部しか移行されない

①の方法で、Googleアカウントへの紐づけを行ったのですが500件くらいのデータのうち30件ほどしか移行されませんでした。ただし、この原因はGoogleコンタクトのページで下記の設定を行うことで解決はしました。

症状１の解決方法：アカウントに紐づけられた連絡先は、Googleコンタクト上では確認できましたが、データの場所が『連絡先』ではなく、『その他の連絡先』となっておりました。ですので、必要な連絡先として共有したいデータについては『連絡先に追加』ボタンがあるので、それをポチっとすればよいのです。

まとめてできるといいのですが、ちょっとわからなかったので、ひたすらポチポチしていきました。

症状２：メールアドレスしか移行されていない

症状１でポチポチする前に気づくべきだったのですが、必要なデータを全て連絡先に追加した後、肝心のデータがひさんな状態であることに気づきました。あるはずのデータのうち、電話番号が全く移行されておりませんでした。てか、そもそもGoogleコンタクトにすら電話番号が移行されていませんでした。

何かしら原因があるのかもしれないのですが、ちょっと調べた限りよく分からなかったので①の方法は諦めることにしました・・・。

別の方法を模索

残る方法は②と③ですが、②はクラウドに個人データをあげるのに抵抗があったので今回はパス。仕方なく③のアナログ方法をとることにしました。

③をもう少しだけ具体的に書くと以下（詳細は略）

android スマホの電話帳アプリのサブメニューから電話帳データ(***.vcf)をmicroSDに保存（エクスポート）
カードリーダー等を使って、microSDをPCに読み込ませる
電話帳データ(***.vcf)をメールに添付してiphoneに送付
iphoneで受け取ったら添付ファイルをタップし、連絡先に追加

ここで、③の手順がandroidがモバイル通信とかwi-fiに繋がらない状況になっていることを想定しているということに気づきます。

wifi使えるならPCに移行する必要なし

私の場合、①の方法をとろうとしてましたのでwi-fiがあります。つまりandroid スマホもiphoneもwi-fi使えるしgmail使えます。ですので、③の手順2のようにmicroSDに保存したデータをわざわざPCに移行しなくても、gmailでiphoneに電話帳データを送付し、手順４で完了

無事、電話番号＋メアド付きのデータをiphoneに移行することができました

やったことまとめ

android スマホで電話帳データ(**.vcf)をmicroSDカードにエクスポート（たぶん本体容量が大きい場合、microSDカードなくてもいいのかも）
androidからiphoneにgmailで電話帳データ（**.vcf）を添付ファイルとして送付
iphoneで添付ファイルをタップ

以上です。詰まったかたは参考にしてください。

2019-03-16

強化学習：再・迷路問題２（Q学習、線形関数近似）

関数近似強化学習 Q学習 Reinforcement Learning 迷路問題

f:id:shirakonotempura:20190314233006p:plain

では、前回の記事に引き続き線形関数近似を使った迷路問題を扱っていきます．
今回はまとめきる予定です．コードは写経が多いので余り見せられるものではないのですが、公開する予定です．

shirakonotempura.hatenablog.com

！！これは私の勉強用ノートです！！

はじめに

前回の続きなので、細かいことは省いていきます．
その２となる今回は、迷路問題についてざっくり説明を行い、学習条件などを整理して、結果まで一気にいきます．
かなり残念な結果が出ているのですが気にしない．これから考えます．

迷路問題をざっくりおさらい

学習の対象とする迷路問題についてざっくりと概要を示します．（このときの設定とほぼ同じです）

f:id:shirakonotempura:20190209000458p:plain

環境は上に示す6×9マスの格子世界の迷路
図中Sはスタート地点、Gはゴールを示しています．グレーのマスは通過できない壁を意味します．
エージェントの行動は4種類（Up, Down, Left, Right）
壁のある方向または迷路外へ動こうとする場合は、その場にとどまり１ステップが経過します．
報酬はゴールに到達する行動に対してのみ＋１が与えられ、それ以外は０とします．（つまり、壁にぶつかろうが、ゴールまでのステップ数が多かろうがぺナルディはありません）
ゴールに到達したらエピソードは終了し、スタート地点に戻り次のエピソードがスタートします

実装

細かい説明は省略し、関数近似の部分についてのみ説明をしていきます．

近似関数および基底関数の設定

価値関数の近似は、線形近似で行います．よって行動価値 $\hat q(s, a ; \boldsymbol{w})$ は以下のように書けます．

$$ \hat q(s,a ; \boldsymbol{w}) = \boldsymbol{w} \boldsymbol{\phi}^T$$

ここで、 $\boldsymbol{w}$ は求めるパラメータ $[w_1, w_2. \cdots, w_N$ ]、 $\boldsymbol{\phi}$ は基底関数 $[\phi_1, \phi_2, \cdots , \phi_N$ ]を示します．

基底関数には、前回の説明で扱ったガウス分布を用います．

いくつ関数を組み合わせるかという点については、余り深く考えずにグリッドの数を使いました．今回のケースでは６×９=５４個の基底関数を使います．基底関数の分布の中心もグリッドの座標を使いました．分散は0.05で固定としています．この辺の設定が良くないのかもしれません．

近似関数のイメージを以下に示します．左図はパラメータを全て１にした場合の局面、右図がパラメータを適当に与えた場合の曲面になります．

f:id:shirakonotempura:20190315073956p:plain

５４個の基底関数をセットしたので、近似関数に対して求めるパラメータの数も５４個になるのですが、厳密にいうと下図右の手法（※）を用いているので５４ ×４のパラメータを計算していることになります．

f:id:shirakonotempura:20190213035604p:plain

※：状態 $s$ を入力にして、行動 $a_m$ の数だけ行動価値を関数 $\hat q (s,a_m,w)$ で表す方法

行動 $a$ も含めた関数にすることも考えられますが、ちょっと３変数を入力とするガウス分布の式が良く分からず断念しました．
基底関数の形状は何でもいいと割りきってしまえば、３変数を入力とするそれっぽい式に改良すればいいだけだとは思いますが．

コード部

基底関数の定義、ｑ値の計算および行動選択部分のコードを示します．

class LinearFunc:
    
    maze = Maze() # 迷路の情報を持つコンストラクタ
    # episodes数以外は、共通
    params = DynaParams() # パラメータ情報を持つコンストラクタ
    
    N1 = maze.WORLD_WIDTH # X方向のグリッド数
    N2 = maze.WORLD_HEIGHT # Y方向のグリッド数
    
    eps = params.epsilon # 探索割合：ε
    gamma = params.gamma # 割引率
    alpha = params.alpha # 学習率
    
    ts = 2 # total states # 基底関数に使う入力変数の数
    NUM_ACTION = 4 # エージェントがとる行動の数

    # 基底関数の中心（μ）をリストで作っておく
    # 中心は、座標のインデックス[X, Y]の組み合わせ
    myu_dist_wid = np.linspace(0.0, N1-1, N1)
    myu_dist_hei = np.linspace(0.0, N2-1, N2)
：
省略
：
    # 基底関数の計算
    # 入力:状態（X座標とY座標）
    # 出力:基底関数の出力*４行動分
    def rbfs(self, s):
        s = s.reshape(len(s),1) # 2次元配列に整形
        return np.exp(-np.square(LA.norm((self.mu_list-s)/self.norm_factor, axis=1))/(2*self.var)) 

    # φ×ωでQ値を計算する関数
    def getQ(self, s, a):
        return (self.rbfs(s)[a]).dot(self.omega_list[a])

    def select_action(self, s):
        # e-greedyによる行動選択   
        if np.random.rand() < self.eps:
            action = np.random.randint(self.NUM_ACTION)
            return action
        else:
            # getQで、各行動に対する近似計算値qs = q(s)を取得
            qs = [self.getQ(s,i) for i in range(self.NUM_ACTION)]
            # qsの中でqs(a)が最大となるaを選択
            action = np.argmax(qs)
            # qsが2つ以上ある場合は、その中でランダムに選ぶ
            is_greedy_index = np.where(qs == action)[0]
            if len(is_greedy_index) > 1:
                action = np.random.choice(is_greedy_index)
            return action

学習条件の設定

学習・パラメータ更新に関する値は以下のように設定します．

割引率は0.9
学習率αは0.1（固定）
行動選択はε-greedy法で行い、εは0.05（固定）
1000エピソードを1エポックとし、同じ条件で3エポックの学習を行う．

1エピソードごとに、ゴールに至るまでに要したステップ数を記録しておき、3エポックの平均をグラフ化する．

ほぼ同じ条件でTabular型のQ学習による学習を行い、結果の比較を行います．

超絶注意：
前回のプランニングのケースのコードをベースに関数近似部分を追加しています．プランニングモデルは更新にQ学習を使っているのですが、今回追加した関数近似の関数の更新は以下のOn-line 更新を使っています．比較と言いつつ更新の考え方が異なっています．気づいたときには、修正する気力がありませんでした．ご容赦ください・・・．

$$\boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[R_{t+1} + \gamma \hat{q}_(s_{t+1}, a_{t+1}:\boldsymbol{w}) - \hat{q}(s_t, a_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{q}(s_t, a_t; \boldsymbol{w}_t)$$

Sutton本　p.244 (10.2)式より

パラメータの更新

パラメータ $w$ の更新部分のコードを示します．

# パラメータθの更新
def train(self, s, a, reward, s_dash, a_dash):
    phi = self.rbfs(s)
    Q_val = self.getQ(s,a)
    Q_val_dash = self.getQ(s_dash,a_dash)

    DELTA = reward + self.gamma*Q_val_dash - Q_val
    # パラメータの更新式
    self.omega_list[a] = self.omega_list[a] + self.alpha * DELTA * phi[a]

結果（Q学習 vs 関数近似）

勢いでやったせいなのか、全然よくありませんでした．どちらかというとQ学習の方がよさげな結果となっています．最小ステップ数は１４のはずなのですが、どちらも少し上で収束しているように見えますね．

f:id:shirakonotempura:20190316032842p:plain

学習による推定最適経路を図化してみました．Q学習の方は上から周るルートを選択してしまっています．一方の関数近似の方は壁に突っ込んでいく始末．これはどう解釈すべきなのだろうか．報酬の問題でしょうか．コーディングの問題という可能性も大いにあります．

1000 episode学習後の推定最適経路

f:id:shirakonotempura:20190316032855p:plain

今回はεをけっこう小さめの値で固定していますが、最初はもっとランダムに行動させるように、εを段々小さくしていくやり方の方がよいのかもしれません．

こんな結果なので、参考になりもしませんが、Colaboratory上のノートはコチラに置いておきます．
ついでに、３次元ガウス分布のノートも置いておきます．
いずれもかなり汚いので、その点はご了承ください．

まとめ

迷路問題の経路探索を関数近似を用いて行いました．

テーブル型のQ学習による結果と比較してみましたが、いまいち関数近似のメリットが感じにくい結果となりました．何より関数近似の方は、最適経路以外の部分の行動推定値がひどい有様でした．無理やり関数に落とし込むっていうことはそういう可能性を含んでいるということなのかもしれません．

迷路問題のように状態が離散値で得られる場合は関数近似が向いていないのでしょうか？またもや消化不良なものが増えてしまった気がします．どうなるかわかりませんが、行動も関数にいれたバージョンも試してみようかなとは思っています．

2019-03-15

強化学習：再・迷路問題１（Q学習、線形関数近似）

関数近似強化学習 Reinforcement Learning Q学習迷路問題

春休みなどもあり少し間が空きましたが、引き続き強化学習についていろいろ書いていきます．
先に書いておくと、今回の記事では迷路の内容まで至っていません．

！！これは私の勉強用ノートです！！

はじめに

今回の主な目的は、線形関数近似の実装です．
というのも、これまでの記事で関数近似の理論について整理してきましたが、具体的なことをやっていなかったので実はよくイメージがつかめていませんでした．

強化学習：関数近似（その１：導入） - 他力本願で生き抜く（本気）

強化学習：関数近似（勾配法とか） - 他力本願で生き抜く（本気）

強化学習：関数近似（パラメータの更新） - 他力本願で生き抜く（本気）

そこで具体的に何かやろうということで、プランニングのときに扱った迷路問題を少し改良して、関数近似で学習するということをしていきたいと思います．といっても、タイトルにあるとおり、線形関数近似になります．

以下、線形の関数近似の復習からはじめて説明していきます．
一応Sutton本だと9.4章あたりの範囲になるかと思います．

線形近似をおさらい

関数近似は、表形式（Tabular）で扱っていた価値関数を $\boldsymbol{w}$ をパラメータに持つ関数（ $\hat v(s,\boldsymbol{w})$ や $\hat q(s,a; \boldsymbol{w})$ ）で表現してしまおうというものでした．その中でも最もベーシックな近似の方法が以下(1)式で示す表現方法になります．今回の記事では行動価値を関数近似で表現することを扱いますので、以降の数式も行動価値を対象にしています．

$$ \hat q(s,a; \boldsymbol{w}) = w_1 \phi_1 + w_2 \phi_2+ \cdots + w_N \phi_N \qquad \qquad \cdots \qquad (1)$$

ここで、 $\phi$ は基底関数を表します．基底関数とパラメータ $\boldsymbol{w}$ が一次線形結合でつながっているので、この近似方法を線形近似と呼びます．

(1)式をベクトル表現を使って書き直すと以下のように書くことができます．

$$ \hat q(s,a; \boldsymbol{w}) = \boldsymbol{w} \boldsymbol{\phi}^T \qquad \qquad \cdots \qquad (2)$$

ここで、 $\boldsymbol{w}$ および $\boldsymbol{\phi}$ は、それぞれ以下のようなベクトルを意味しています．

$\qquad \boldsymbol{w} = [w_1, w_2, \cdots , w_N$ ]
$\qquad \boldsymbol{\phi} = [\phi_1, \phi_2, \cdots , \phi_N$ ]

これで、行動価値を線形近似の形で示すことができました．

関数の表現力について

上記で示した式中のNの値、つまり基底関数の数が増えれば、この関数の表現力は高くなります．
関数の表現力というのは、この関数がどのくらいいろんな値を返すことができるかということなのですが、少し図を使って表現力について考えてみます

例として分散=0.5（固定）としたガウス分布の図を例にして線形近似関数が示す関数の形状を見ていきます．なお、このガウス関数の値 $z$ は、分布の中心を $(\mu_1, \mu_2)$ として、以下の式で計算しています．

$z = \exp \biggl( - \frac{(x-\mu_1)^2 + (y-\mu_2)^2}{2\sigma^2} \biggr)$

基底関数1つの例：
どんなに頑張ってパラメータを調整しても、ガウス関数のベル型の形状を表現することしかできません．
基底関数4つの例：
パラメータを調整すれば、基底関数が１つだった場合と比べると複雑な形状を示すことができそうです．しかし、パラメータを変えたところでほとんど変化しないところもまだまだあります．
基底関数25個：
これくらいあれば、かなり複雑な形状を示すことができそうな気がします．

基底関数にどんな関数を選んで、Nをどの程度にするかということは、人が決める必要があります． Nが少なすぎるといくら学習を繰り返してたとしても表現できない部分が出てきてしまいますので、けっこう大きな値を設定しておけばいいのかなと思っています．もちろんその分計算負荷は増えますので、時間がかかりすぎるようであれば減らしていく必要があります．

パラメータの更新における線形近似のメリットについて

以前の記事の最後に、パラメータ[\tex:\boldsymbol{w}]の更新式を以下のように書きました．

パラメータ更新に関する詳細は今回は省きますが、この式の末尾にある $\nabla \hat{q}(s_t, a_t; \boldsymbol{w}_t)$ の部分は、近似関数 $\hat{q}$ のパラメータ $\boldsymbol{w}$ による偏微分を示しています．仮定した近似関数の微分が簡単に求められればいいのですが、複雑な関数を仮定すればするほど微分の計算は複雑になってきます．ここで、線形近似のメリットが現れます．

線形近似で表現した行動価値の近似関数 $\hat{q}$ をもう一度以下に示します．簡単のため、 $\hat q(s,a; \boldsymbol{w})$ は $\hat q$ とだけ表します．

$$ \hat q(s,a; \boldsymbol{w}) = w_1 \phi_1 + w_2 \phi_2+ \cdots + w_N \phi_N \qquad \qquad \cdots \qquad (1)$$

この式をパラメータ $\boldsymbol{w}$ で偏微分するということは、以下のような計算を行うことになります．

$$ \frac{\partial \hat q}{\partial \boldsymbol{w}} = \biggl[ \frac{\partial \hat q}{\partial w_1}, \frac{\partial \hat q}{\partial w_2}, \cdots, \frac{\partial \hat q}{\partial w_N} \biggr] \qquad \qquad \cdots \qquad (4)$$

(4)式中の $\frac{\partial \hat q}{\partial w_1}$ を詳細に見てみます．

$$\frac{\partial \hat q}{\partial w_1} = \frac{w_1 \phi_1}{w_1} + \frac{w_2 \phi_2}{w_1}+ \cdots + \frac{w_N \phi_N}{w_1}\qquad \qquad \cdots \qquad (5)$$

くどいですが、(5)式は $\hat q$ を $w_1$ による微分を示しています．第1項以外は $w_1$ に関してみれば、定数項になりますので $w_1$ で微分すれば0になり、 $\phi_1$ だけが残ることになります．
同様にして、 $\hat q$ を $w_2$ 、 $w_3$ 、・・・ $w_N$ で微分を考えると、(4)式は以下のように基底関数そのものになります．

$$ \frac{\partial \hat q}{\partial \boldsymbol{w}} = \biggl[ \phi_1, \phi_2, \cdots \phi_N \biggr] \qquad \qquad \cdots \qquad (6)$$

これにより関数近似に線形近似を用いた場合、(3)式で示したパラメータの更新式は(7)式のように書くことができます．

このように、仮定した近似関数の微分を計算しなくてもよいという簡便さが線形近似の大きなメリットになります．

本当は迷路まで一気にまとめてしまいたかったのですが、一旦区切ります．

まとめ

迷路問題に対する線形関数近似の実装に向けて、線形近似部分の説明のみを行いました．
実はなんか計算がうまくいっていないのですが、次回は一気に、迷路問題の解説・結果までを記事にしたいと思います．

以下の記事を参考にさせていただきました．式展開の部分はほぼトレースです．

qiita.com

2019-02-23

強化学習：Taxi-v2（Q-Learning, SARSA, Expected SARSA）

強化学習 TD学習 Q学習 SARSA Expected SARSA Taxi-v2

2019.2.25　追記：SARSAおよびExpected SARSAのコーディングに誤りがあります．修正したら記事も修正するか別の記事で修正版を出すようにします．

はじめに

今回は、以前やった内容の復習が主になります．
タイトルにあるとおり、TD学習の手法であるQ学習、SARSAおよびExpected SARSAの３つを実装してみて、結果の比較を行います．

Q学習、SARSAは以前扱った内容なので、理論の説明は少な目、コード多めになる予定です．

shirakonotempura.hatenablog.com

これは、私の学習用ノート．メモ、備忘録です

Open AI Gym

今回の学習ではOpen AI Gymを利用しています．

Open AI Gymは、強化学習の研究者向けに提供されている開発環境で、自分で学習させたAI（エージェント）を実際に動かすことができるシミュレータを提供してくれます．Cart PoleやMountan Carなどは有名なので見られたことがあるかと思います．

f:id:shirakonotempura:20190223040602p:plain

今回はその中から、Taxi-v2を使ってみたいと思います．

Taxi-v2

Taxi-v2ではタクシー運転手が乗客をピックアップして、降車させるタスクを扱います．
学習の目的は、ちゃんとした場所で乗客を乗せ、できるだけ短い距離を通って目的地に連れていくことです。

環境

フィールドは、以下に示す５×５の格子世界になります． - 黄色いシンボルがタクシーを示しており、乗客をピックアップすれば緑色に変わります． - R, G, B, Yの文字が示された4マスのいずれかが、乗客の位置および目的地となります． - " | " は壁を意味しており、そこを通りぬけることはできません．

f:id:shirakonotempura:20190223042509p:plain

状態について

まず状態 $s$ について説明します．

これまで扱ってきたようなGrid Worldの問題ではグリッド数＝状態数であることが多いのですが、今回は少し異なります．

乗車位置、目的地がエピソードごとに変化するということは、同じマスであっても取るべき行動は変わってきます．そこで、乗車位置と目的地も状態を表す要素の１つと考えることで以下のように考えることができます．

５（縦）×５（横）×４（乗車位置）×４（目的地）＝４００（総状態数）

実はこれでは不十分で、このままでは、乗客を乗せる前と後で同じ状態が現れてしまいます．そこで、乗車位置を乗客の位置にしてしまい車の中という状況を加えることで、同じ環境で乗車前と乗車後を考えることができます．

５（縦）×５（横）×５（乗客の場所）×４（目的地）＝５００（総状態数）

行動について

次に行動[text:a]について説明します．

格子世界なので、移動アクションは上下左右の4方向を考えます．これまでと違う点として、乗客のピックアップ（pick up）および降車（drop off）がこれに加わり、行動は全部で６種類となります．

Taxi-v2で与えられた順番と名前のとおりに書くと以下のようになります．

行動 $a$ = ["South", "North", "East", "West", "Pickup", "Dropoff"]

報酬とエピソードの終了について

最後に報酬について説明します．

乗客を目的地まで運ぶことで報酬＋２０を受け取ります．
乗客のいない場所でpick upの行動をとると‐１０の報酬を受け取ります．
目的地でない場所、乗客がいない状態でdrop offの行動をとった場合も‐１０の報酬を受け取ります．
１マス進むたびに‐１の報酬を受け取ります

乗客を目的地で降車した場合エピソードが終了し、タクシーの位置、乗客の位置、目的地がランダムに決められます．
‐１０の報酬を受け取る行動をとったとしても、エピソードは終了しません．

ただし、２００ステップが経過した時点でエピソードは強制的に終了となります．（デフォルトの設定）．これは環境を定義する際に回避することもできるようですが、時間がかかる場合もありますので個々の判断にお任せします．（私はデフォルトのままにしてます）

上限を２００ステップにした環境設定方法 env = gym.make("Taxi-v2")
２００ステップの制限なしの環境設定方法 env = gym.make("Taxi-v2").env

やっとTaxi-v2の説明が終わりました・・．長くなってしまいました．

学習アルゴリズム（Qテーブルの更新式）

前回、関数近似について整理しましたが、今回は単純にQテーブルを使って行動価値 $Q(s,a)$ の更新を行っていきます．

まずは、以下に、Q学習とSARSAのQテーブルの更新式を示します．

Q-Learning $$Q(s, a) \leftarrow Q(s, a) + \alpha [R + \gamma \; argmax_{A} Q(s', a) - Q(s, a)]$$
SARSA $$Q(s, a) \leftarrow Q(s, a) + \alpha [R + \gamma Q(s', a') - Q(s, a)]$$

Q-Learningの場合は、次の状態 $s'$ における最も高い行動価値 $\; argmax_{A} Q(s', a)$ を更新式に使い、SARSAでは方策に従って実際に選択した行動の行動価値 $Q(s', a')$ を更新式に使っていました．~~（１ステップで２回行動するわけではありません．あくまで選択したという仮定です）~~

2019.2.25追記
1ステップに２回行動するわけではないですが、選択した行動 $a'$ は、次のステップの行動になります．間違っていました．
コードは、次のステップでまた行動選択をsoftmax法で行っているので、誤っています．すいません．

Expected SARSAについて

Expected SARSAについてはこれまで説明してこなかったのですが、上の２つと大きく変わりません．

Expected SARSA $$Q(s, a) \leftarrow Q(s, a) + \alpha [R + \gamma \sum_{a} \pi (s', ) Q(s', a) - Q(s, a)]$$

$\sum_{a} \pi (s', ) Q(s', a)$ の部分が、Expectedの名前のとおり状態 $s'$ における行動価値の期待値を示しています．

行動選択方法→温度付きsoftmax行動選択法

もう１つこれまでと違うことをやっているので、簡単に説明します．

これまでは行動選択にε-greedy法を用いてきました．ε-greedy法は、確率1-εでこれまでで最良の行動を選び、確率εでランダムに行動を選択するというものでした．

今回は、softmax関数を使った行動選択方法を採用しています． softmax関数は、多クラス分類問題において、そのクラスである確率を計算するときに使われる関数です．

具体的な数式を以下に示します． $$\pi(Q(s, a_i))= \frac {e^{Q(s, a_i)}} {\sum {e^{Q(s, a)}}}$$

左辺の $\pi(Q(s, a_i))$ が状態 $s$ が、行動 $a_i$ を選ぶ確率になります．
この式を直接使うことも可能ですが、今回は上記の式を若干修正した、温度付きsoftmax関数を使用します．

$$\pi(Q(s, a_i))= \frac {e^{\frac{Q(s, a_i)}{T}}} {\sum {e^{\frac{Q(s, a)}{T}}}}$$

ここでTは温度パラメータで、Tが大きいほど確率の差が縮まり（ランダム性が強くなり）、Tが小さいほど高い確率が強調される（greedyな行動選択）ようになります．ステップ数やエピソード数を温度の変数に使うことで、学習初期はランダム性を高めたりすることができます．

温度付きsoftmax関数について、もう詳しく見たい方は以下の記事を参考にしてください

温度付きsoftmax 覚書 - Qiita

実装

では、実装した内容とについて説明します．パラメータである温度と学習率の影響も見たかったので、パラメータスタディができるようにしています．

共通条件
- １０エピソードを１セグメントとし、１００セグメントで１タスクとしています．
- １つの学習タスクに対して、同じ条件の検討を10回行い、平均値をプロットするようにしています
- 更新時の割引率 $\gamma$ は0.8
- 学習率は0.01および0.2
- 温度は0.2および2.0

学習部分

学習部分のコードは以下に示します．
見ればわかると思いますが、パラメータごとにfor文で回しまくってます．見た目はいまいちですね．
１セグメント終わるごとに、あらかじめ用意しておいた空の配列リストに必要な結果をappendし、１タスクが終わればQテーブル(q_table)を初期化しています．

# TRAINING PHASE
for episode in range(episodes):
    #initiralize
    state = env.reset()
    steps, penalties, reward, = 0, 0, 0
    total_rewards = 0
    done = False
                    
    # Loop for 1 episode(max 200 steps in default)
    while not done:
                        
        #Choose Softmax
        act_prob = softmax(q_table[state], temper)
        action = np.random.choice(len(q_table[state]), p= act_prob)
               
        # Get reward, next_s
        next_state, reward, done, info = env.step(action)
                  
        # Count Penalty (for illegal pickup and drop off)
        if reward == -10: #bad perform gets negative reward and penalty
            penalties += 1

        # common data for updating
        old_value = q_table[state, action]
        act_prob_n = softmax(q_table[next_state], temper)
            
        # update action_value(q_learning)
        if method == "q_learn":
            next_max = np.max(q_table[next_state])
            new_value = old_value + alpha * (reward + gamma * next_max - old_value)
                        
        # update action_value (sarsa) 
        elif method == "sarsa":
            action_n = np.random.choice(len(q_table[next_state]), p= act_prob_n)
            new_value = old_value + alpha * (reward + gamma * q_table[next_state, action_n] - old_value)
                            
        # update action_value (ex_sarsa)
        elif method == "ex_sarsa":
            expected = np.dot(act_prob_n, q_table[next_state])
            new_value = old_value + alpha * (reward + gamma * expected - old_value)
                
        q_table[state, action] = new_value
                          
                            
        # change current state
        state = next_state
        steps += 1
        total_rewards += reward
                    
        # add 10th episode's result to results list
        if episode == episodes -1:
            train_results[i][j][run].append(total_rewards)
    return train_results, test_results

各更新式の部分だけ少し詳細に見ます．

Q-Learning

# update action_value(q_learning)
    if method == "q_learn":
        next_max = np.max(q_table[next_state])
        new_value = old_value + alpha * (reward + gamma * next_max - old_value)

nex_maxで次の状態 $s'$ における最良の行動のQ値を取得し、更新式で使用しています．

SARSA

# update action_value (sarsa) 
    elif method == "sarsa":
        action_n = np.random.choice(len(q_table[next_state]), p= act_prob_n)
        new_value = old_value + alpha * (reward + gamma * q_table[next_state, action_n] - old_value)

SARSAで必要になるのは、次の状態 $s'$ において選択した行動 $a'$ の行動価値なので、まず行動 $a'$ （action_n）の選択を行っています．なお、この行動選択も温度付きsoftmax関数を使って行っています．

Expected SARSA

# update action_value (ex_sarsa)
    elif method == "ex_sarsa":
        expected = np.dot(act_prob_n, q_table[next_state])
        new_value = old_value + alpha * (reward + gamma * expected - old_value)

先に期待値（expected）の計算をしてから、更新を行っています．期待値は次の状態 $s'$ における各行動の選択確率（act_prob_n）×各行動のQ値（q_table[next_state]）で計算しています．当然、選択確率の計算はsoftmax法になります．

全体的にfor ループが多すぎるせいか、めちゃくちゃ遅いです．

colaboratoryのノートはコチラです．

結果

学習結果を示します．

下の図は、Q学習のみでパラメータによる学習曲線の違いを示したものになります．学習率 $\alpha = 0.01$ のケースは学習率が小さすぎて学習の進捗が遅いですね．温度に関してはT=2.0よりはT=0.2としてランダム性を強くした方がよさげですが、では0.2が最適なのかどうかについては、パラスタをして決める必要があります．

f:id:shirakonotempura:20190223072055p:plain

下の図は、3手法による結果を重ね書きしたものです．更新方法ごとの違いが、結果に全然現れてないですね．
これはコーディングが合っているのか不安になるレベルです．

f:id:shirakonotempura:20190223071712p:plain

まとめ

今回はOpen AI gymにあるTaxi-V2を使ってQ学習、SARSA、Expected SARSAの実装を行いました．
比較の部分がまだ改善の余地ありですが、自分でコードを書いてみると手法による計算の違い・共通部分がよくわかりました．
ただし、上記の結果のとおり正しく実装できているのか不安です．

また、前回勉強したクラスを全く使っていませんので、まだまだですね．

もう少し今回の内容を見直した後は、今度こそ関数近似の問題をやるつもりです．

2019-02-20

強化学習：関数近似（パラメータの更新）

関数近似強化学習パラメータ更新

はじめに

前回は、近似式と目標値の差を表す誤差関数を最小化するパラメータの探索手法の１つである勾配法について整理しました．

強化学習：関数近似（勾配法とか） - 他力本願で生き抜く（本気）

今回は、強化学習におけるパラメータの更新について詳しく見ていきます．

この記事は私の学習用ノートです

パラメータ $\boldsymbol{w}$ の更新

以下では、Sutton本に合わせて状態価値関数 $V(s)$ を使って説明しています．もちろん、行動価値関数 $Q(s,a)$ にも関数近似は適用できます．行動価値関数のパラメータ更新については最後に紹介するようにします．

誤差関数（おさらい）

『真の状態価値 $v^* (s)$ 』と『近似式による推定値 $\hat{v}(s,\boldsymbol{w})$ 』を使った誤差関数 $E_{SE}(\boldsymbol{w})$ をあらためて示します．これは、教師あり学習のやり方に沿って定式化したものになります．

$$E_{SE}(\boldsymbol{w}) = \sum_{s}[v^* (s)- \hat{v}(s,\boldsymbol{w})]^2 \qquad \cdots (1)$$

この誤差関数を最小化するパラメータ $\boldsymbol{w}$ を勾配法を使って求めたいのですが、式中 $v^* (s)$ で示した真の価値（教師あり学習で言う正解データ）は、強化学習では与えられません．

そのため、何か真の価値の代わりになるものをターゲットにする必要があるのですが、とりあえずそのままターゲット（ $Target$ ）と呼ぶことにします．

ターゲットは自分で行動して決める

具体的なターゲットの中身は後程説明しますが、どのようにターゲットを決めるかと言うと、強化学習ではこれまでと同じように行動しながら決めることになります．

教師あり学習をベースにした(1)式では複数の正解データが与えらることを想定して誤差の２乗和（ $\sum$ ）を取っていましたが、強化学習における誤差関数は、ターゲットと近似値の差の２乗を毎ステップ、誤差関数として計算することになります．

以上のことから、強化学習における誤差関数は以下の(2)式のように表します．ややこしいので添え字のSEは消しました．

$$E(\boldsymbol{w}) = [Target- \hat{v}(s,\boldsymbol{w})]^2 \qquad \cdots (2)$$

図におけるイメージで説明

では、(2)式を最小化するパラメータ $\boldsymbol{w}$ を求めることになりますが、以下に誤差関数 $E(\boldsymbol{w})$ の更新イメージを示します．

f:id:shirakonotempura:20190216093600p:plain

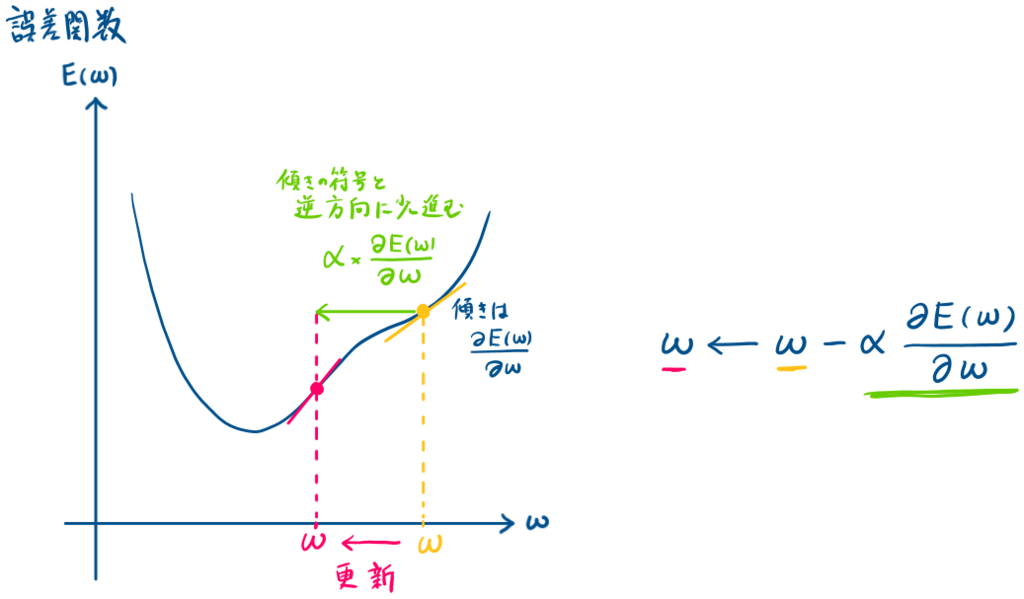
式の導出

正直、導出と呼べるほどのことはしていませんが語彙力不足のため、他の言葉が思い浮かびませんでした．
要は、上のイメージを式で表していくだけです．

上に示したイメージ図から、更新されるパラメータ $E(\boldsymbol{w})$ は(2)式で表すことができます．(3)式中の $\alpha$ は学習率（定数）になります．

$$ \boldsymbol{w}\leftarrow \boldsymbol{w} - \alpha \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}} \qquad \cdots (3)$$

(3)式中の、 $\frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}$ の部分は(2)式で示した誤差関数 $E(\boldsymbol{w})$ のパラメータ $\boldsymbol{w}$ による偏微分を示すので、(2)式を使うと以下のように書くことができ、(4)式が得られます．

$$\begin{eqnarray} \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}} &=& \frac{\partial}{\partial \boldsymbol{w}} \Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr]^2 \\ &=& 2\Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr] \Bigl(- \nabla \hat{v}(s; \boldsymbol{w})\Bigr)\\ &=& -2\Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr] \nabla \hat{v}(s; \boldsymbol{w}) \qquad \cdots (4)\\ \end{eqnarray}$$

(4)式を(3)式に代入すると、以下のように書けます．

$$ \boldsymbol{w} \leftarrow \boldsymbol{w} + 2 \alpha \Bigl[Target - \hat{v}(s; \boldsymbol{w})\Bigr] \nabla \hat{v}(s; \boldsymbol{w}) $$

これで、大方の形は出来上がりましたが、少しだけSutton本に合わせて化粧をします．

まず、 $2\alpha$ は定数になりますので、まとめて $\alpha$ としてしまいます．また時刻 $t$ における状態 $s_{t}$ におけるパラメータ $\boldsymbol{w}_{t}$ の更新という意味で添え字を付けます．

$$ \boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[Target - \hat{v}(s_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{v}(s_t; \boldsymbol{w}_t) \qquad \cdots (5)$$

これで、パラメータ $\boldsymbol{w}$ の更新式の基本の形は完成になります．

Targetについて

いよいよ問題のターゲット（Target）について、説明していきます．

基本的には、これまでのテーブル形式でやってきた更新と考え方は同じです．テーブル型における、TD(0)学習の更新式を以下に示します．（sutton本の(6.2)式）

$$ V(s_t) \leftarrow V(s_t) - \alpha [R_{t+1} + \gamma V(s_{t+1}) - V(s_t)]$$

上記の式における $R_{t+1} + \gamma V(s_{t+1})$ は、報酬 $R_{t+1}$ と遷移後の状態価値 $V(s_{t+1})$ を使った、『状態 $s$ における状態価値 $V(s_t)$ の推定値』になります．学習率を使っているのでいきなり置換するわけではありませんが、これが目標値になっていました．

関数近似においても、同じくこの推定値を目標値と考えることができます．
テーブル型の場合は、 $V(s_{t+1})$ の部分をテーブルを用いて求めていましたが、今回はそこが近似式を使った近似値になるだけです．

つまり、 $V(s_{t+1})$ を $\hat{v}_(s_{t+1}:\boldsymbol{w})$ に置き換えればよく、関数近似における目標値は以下のように表すことができます．

$$R_{t+1} + \gamma \hat{v}_(s_{t+1}:\boldsymbol{w})$$

これを(5)式の $Target$ に代入すれば以下の(6)式が得られます．

$$ \boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[R_{t+1} + \gamma \hat{v}_(s_{t+1}:\boldsymbol{w}) - \hat{v}(s_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{v}(s_t; \boldsymbol{w}_t) \qquad \cdots (6)$$

疑似コード

最後に疑似コードを示します．

f:id:shirakonotempura:20190220024925p:plain

出典：R.Sutton and G Barto, Reinforcement Learning An Introduction, pp.203

行動価値関数への適用（10章、On-Policy Controlの範囲）

ここまで、状態価値関数 $V(s)$ を中心に説明してきましたが、当然、行動価値関数 $Q(s,a)$ も $\boldsymbol{w}$ をパラメータに持つ関数を用いて近似することができます．

行動価値関数では状態 $s$ と行動 $a$ を入力になりますので、(6)式をもとにした行動価値関数のパラメータ更新式は以下のように書くことができます．（Sutton本の10章、(10.2)式に該当します）

$$ \boldsymbol{w_{t+1}} \leftarrow \boldsymbol{w}_{t} + \alpha \Bigl[R_{t+1} + \gamma \hat{q}_(s_{t+1}, a_{t+1}:\boldsymbol{w}) - \hat{q}(s_t, a_t; \boldsymbol{w}_{t})\Bigr] \nabla \hat{q}(s_t, a_t; \boldsymbol{w}_t) \qquad \cdots (7)$$

局所最適解について補足

前回、最適化において局所解に落ち込んでしまうことを問題に挙げました．
しかし、Sutton本の9.2章をよく読んでみると

『理想としては、すべてのパラメータ $\boldsymbol{w}$ に対して誤差関数が最小となる $\bar{VE} ( \boldsymbol{w}^{*} ) \leq \bar{VE}( \boldsymbol{w} )$ となる $\boldsymbol{w}$ * を求めることである．しかし、（中略）それが求まる可能性はほとんどない．』

というようなことが書かれています．これは、あまりGlobal minimumにこだわる必要はなくて、実務的には局所最適解が求まればまずまず．といったことなのかもしれません．

まとめ

今回は、強化学習における関数近似のパラメータ更新について整理しました．

もう少し関数 $v(s,\boldsymbol{w})$ について勉強するか、あるいは何かしら関数近似を使って問題を解くなどもしてみたいですが未定です．

2019-02-14

強化学習：関数近似（勾配法とか）

強化学習関数近似勾配降下法最急降下法 DG SDG

f:id:shirakonotempura:20190213075046j:plain

追記（謝罪）：偏微分の式で分母にしか記号 $\partial$ を付けていませんが、正しくは分子にも必要なようです．以後気を付けます．

はじめに

前回に続き、関数近似について整理していきます．前回は途中で疲れ果ててしまいました・・．

強化学習：関数近似（その１：導入） - 他力本願で生き抜く（本気）

今回は、主にパラメータを更新する際に用いる勾配降下法についての内容となります．これはかなり教師あり学習の内容とかぶりますが、あまり理解してこずに放置していた内容になりますので、いい機会なので整理しておきます．

教師あり学習との類似点と違い

前回説明した基底関数が決まれば、いよいよ近似関数のパラメータ調整に入っていきます．

教師あり学習では、推測値と正解（教師）データの差の2乗和、つまり２乗誤差が小さくなるようにパラメータを更新しました．

強化学習において、推測値に相当するのが近似関数によって出力される価値関数、正解データに相当するものが真の価値関数になります．

つまり、強化学習においては、『真の価値』と『近似関数による推定価値』の２乗誤差を最小化するためにパラメータ $\boldsymbol{w}$ の更新を行っていきます．この枠組みは教師あり学習と同じ考え方です．

f:id:shirakonotempura:20190213081922p:plain

しかし、教師あり学習と決定的に違う点は強化学習においては、当然、真の価値関数は与えられないという点です．そのため、真の価値関数に代わるものを考えなければならないのですが、とりあえずは真の価値関数という表現を使って話をすすめます．

先に言っておくと、真の価値関数の代わりになるものを試行を通じて求め、それを正解データのように扱うということで学習は進んでいきます．この辺は、次回以降もう少し詳しく説明する予定です．

f:id:shirakonotempura:20190213082748p:plain

二乗誤差の計算

話を簡単にするため、以降では状態価値関数に話を限定して

真の価値関数を $v^*(s)$
関数近似による推定価値関数を $\hat{v}(s, \boldsymbol{w})$

とします．

この記号を使えば、２乗誤差（Squared Error）は以下のように定義できます．

$$E_{SE}(\boldsymbol{w}) = \sum_{s}[v^* (s)- \hat{v}(s,\boldsymbol{w})]^2$$

教師あり学習であれば、次に $E_{SE}$ の勾配を求めるため、 $E_{SE}$ をパラメータ $\boldsymbol{w}$ で微分してという流れになるのですが、ここは一旦これで止めておきます．

◇◇ 悩み中（On Policy Distributionについて) ◇◇

Sutton本9.2章に以下の式が(9.1)式として出てきます．

$$\bar{VE}(\boldsymbol{w}) \dot{=} \sum_{s \in S} \mu(s) [v_\pi(s) - \hat{v}(s,\boldsymbol{w})]^2$$

右辺は各状態 $s$ における二乗誤差の総和を表しているのですが、右辺の $\mu(s)$ がどうしても理解できません．on-policy distribution と呼ぶみたいですが、ある状態 $s$ の重みでしょうか？引き続き理解に向けて勉強しますが、万が一、詳しい方が見ていれば教えてください・・．

関数近似と勾配法

さて、強化学習におけるパラメータ $\boldsymbol{w}$ の更新に関する内容は次回以降に回すことにしましたので、ここでは近似を行う方法に関して、もう少し一般的な話をしたいと思います．
先に書いたように、近似にはターゲットが必要となりますので、ここではターゲットとして、正解データが与えられた教師あり学習を例に挙げて説明します．

例題

f:id:shirakonotempura:20190214010046p:plain

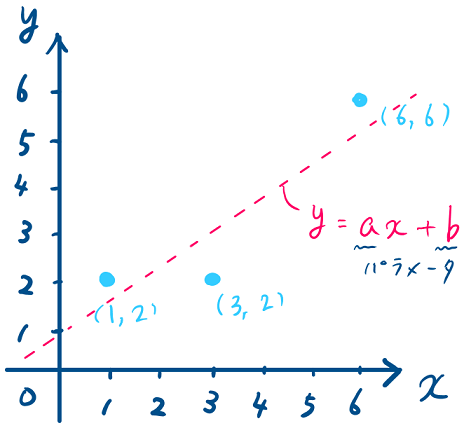
上記に示した水色の３点を $y = ax + b$ の１次式で近似することを考えます．この場合、求めたいパラメータは $a$ および $b$ の２つになります．

手計算でやってみる

最初に手計算でパラメータを求めてみたいと思います．

手計算であろうと勾配法であろうと、最初にやることは誤差関数を求めることになります．

f:id:shirakonotempura:20190214013731p:plain

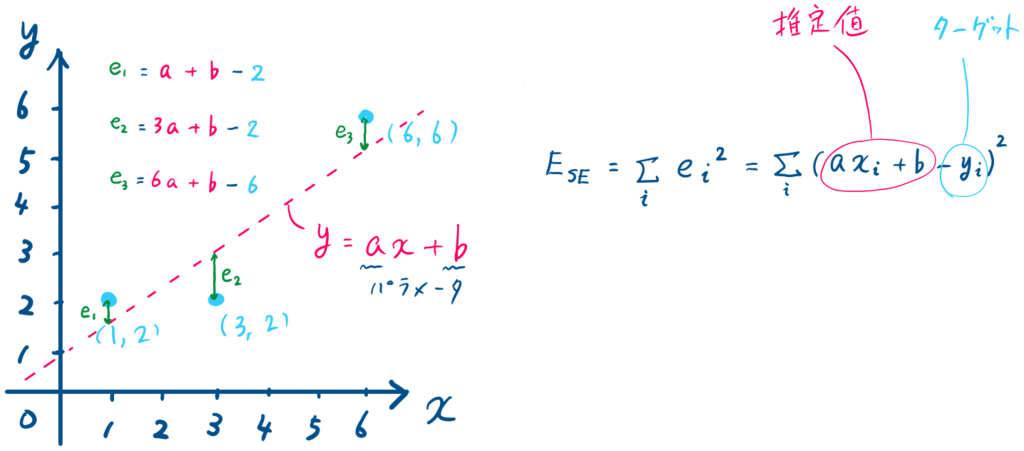
$a,b$ をパラメータとする誤差関数 $E_{SE}(a, b)$ はターゲットと推定値の差（図中の $e_{i}$ )の総和となり、式を展開すると以下のようになります．

$E_{SE}(a,b) = 46a^2 + 3b^2 + 20ab - 88a -20b +44\qquad \cdots (1)$

この誤差関数が最小となるようにパラメータ $a,b$ を求めます．
$E_{SE}(a,b)$ が最小となるのは、(1)式を $a,b$ でそれぞれ偏微分した $\frac{E(a,b)}{\partial a}$ 、 $\frac{E(a,b)}{\partial b}$ が０となるとき（※1）なので、以下の連立方程式を解くことでパラメータ $a,b$ を計算することができます．

$\frac{E(a,b)}{\partial a} = 92a + 20b - 88 = 0$
$\frac{E(a,b)}{\partial b} = 20a + 6b -20 = 0$

（もうちょいましな係数にすべきだったと後悔）

これを解くと、 $a \fallingdotseq 0.842$ 、 $b \fallingdotseq 0.526$ が得られます．

※1：
誤差関数 $E(a,b)$ を $a$ で偏微分する場合、パラメータ $b$ は定数扱いになり、 $E(a,b)$ は下に凸の２次関数 $E(a)$ とみなせます．そのため、微分して得られる傾きが０となる点は関数 $E(a)$ の谷底となり、その点は $E(a)$ を最小化する $a$ になります．同様にして、関数 $E(b)$ を最小にするパラメータ $b$ も計算することができます．

f:id:shirakonotempura:20190214023244p:plain

（この絵はイメージのため、都合よく書いています．誤差関数は極値（谷とか山になる頂点）が複数あることがほとんどです）

勾配法でやってみる

次に、勾配法（Gradient Method）を使ってパラメータを求めてみます．

勾配法は最適化手法の一つで、あるパラメータを持つ評価関数が最小や最大になるときのパラメータを求めることができます．上の例題は、問題設定が簡単なので手計算で解けてしまいましたが、関数の表現力をあげると、パラメータの数も増えることになりますので、一般的に手計算では手に負えません．

まずは、おそらく一番ベーシックな最急降下法と呼ばれる手法について紹介し、次にそれにランダム性を加えた確率的勾配降下法を紹介したいと思います.

◇◇ 補足（雑談）◇◇

パラメータ $\boldsymbol{w}$ や $\boldsymbol{\theta}$ の更新に使う勾配降下法ですが、勾配降下法と最急降下法といいう言葉が混同されていることがあります．

個人的には、勾配降下法（または勾配法、Gradient Method）の具体的な方法の１つが最急降下法（Gradient Descent）であったり、次に説明する確率的勾配降下法（Stochastic Gradient Descent）となるという理解です．たぶんこれはあっているはずです．
ただ、確率的勾配降下法はランダムにピックしたサンプルに対して最急降下法の適用を繰り返すことだと思うので、確率的最急降下法と呼ぶべきなんじゃないかと思っています．とはいえ、なじみのない言葉を使っても仕方ありませんので、SGDは確率的勾配降下法として説明していきます．

この記事では、勾配降下法は傾きを使ってパラメータの更新を行う方法全般のことを指し、最急降下法（GD）、確率的勾配降下法（SGD）は具体的な手法の１つを指すものとします。

最急降下法（Gradient Method）

最急降下法は、ざっくり言ってしまえば、傾きと逆の方向にちょっとだけ進むことを繰り返す方法です．アルゴリズムは非常にシンプルです．

最小化したい誤差関数 $E_{SE}(a,b)$ は先ほど式(1)で示したものですが、パラメータ $a,b$ をまとめてベクトル $\boldsymbol{w} = (a, b)^T$ を使って表すことにします．

誤差関数 $E_{SE}$ を $\boldsymbol{w}$ で偏微分する
- 要は、 $E_{SE}$ を $a$ および $b$ で偏微分することなので、手計算のときに出てきた連立方程式のことです．
適当にパラメータ $\boldsymbol{w}$ を決める
- 適当に $a$ および $b$ を選びます．これがパラメータの初期値になります．
現在のパラメータを使って誤差関数 $\boldsymbol{w}$ の傾き $\frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}$ （=勾配ベクトル）を求める
- 具体的には、1.の連立方程式に2.で決めた $a$ と $b$ を代入します．
- つまり現在の位置における勾配を求めていることになります．
最急降下方向に進む（勾配ベクトルの符号と逆方向）
- ここが先に書いた、逆方向にちょっとだけ進むに相当します．
- 3.で計算した勾配ベクトルに沿って、最も小さくなる方向（最急降下方向）に動きたいのですが、その方向は勾配ベクトルと符号が逆になります．
- よって、以下の式でパラメータ $\boldsymbol{w}$ を更新します．（式中の $\alpha$ は学習率で0.01や0.05のような値が使われます．） $$\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \frac{\partial E(\boldsymbol{w})}{\partial \boldsymbol{w}}$$
- 今回の例で、もう少し具体的に書くと $$a \leftarrow a - \alpha \frac{\partial E(\boldsymbol{w})}{\partial a}$$ $$b \leftarrow b - \alpha \frac{\partial E(\boldsymbol{w})}{\partial b}$$
$\boldsymbol{w}$ が収束するまで、上記3と4を繰り返す

f:id:shirakonotempura:20190214064120p:plain

ちょっと図がごちゃごちゃしてますが、右図は左の図の一部を拡大したと思ってください．

このように最急降下法では反復計算によって、パラメータの推定を行います．
そのため先の例を最急降下法で解こうとすると、この紙面では足りないので一部省略しますが、次のような計算を繰り返すことになります（学習率 $\alpha=0.01$ としています）．

$E(\boldsymbol{w})/\partial a = 92a + 20b - 88$
$E(\boldsymbol{w})/\partial a = 20a + 6b - 20$

t=0
$a = 0$ , $b = 0$
$E(\boldsymbol{w})/ \partial a = 92 * 0 + 20 * 0 - 88 = - 88$
$E(\boldsymbol{w})/ \partial b = 20 * 0 + 6 * 0 - 20 = - 20$
$a \leftarrow 0 - 0.01 * (-88) = 0.88$
$b \leftarrow 0 - 0.01 * (-20) = 0.20$
t=1
$a = -0.88$ , $b = -0.20$
$E(\boldsymbol{w}/\partial a = 92 * 0.88 + 20 * 0.20 - 88 = - 3.04$
$E(\boldsymbol{w}/\partial b = 20 * 0.88 + 6 * 0.20 - 20 = - 1.2$
$a \leftarrow 0 - 0.01 * (-3.04) = 0.9104$
$b \leftarrow 0 - 0.01 * (-1.2) = 0.212$
：

こんな感じで、反復計算を続けていけば３５０ステップくらいで $a = 0.842$ 、 $b = 0.526$ に収束します．

確率的勾配降下法（Stochastic Gradient Method）

では、次に確率的勾配降下法について説明します．これは英語の頭文字を取ってSGDと呼ばれたりします．こっちはさらっと行きます．

この方法は、簡単に言えば、最急降下法にランダム性を持たせたものになります．

これまでの説明において誤差関数 $E(\boldsymbol{w})$ は、ターゲットと推定値の誤差の総和としてきました．つまり、誤差関数 $E(\boldsymbol{w})$ を計算するためには全てのデータが必要でした．
それに対し、SDGでは誤差関数の計算にはサンプルデータ１つを使います．ただし、どれをサンプルに使うかは各反復でランダムに選びます．

サンプルデータを１つしか使わないということは、なかなか収束しないような気がするのですがこれでうまくいくようです．サンプルが３つしかない今回の例題は例外でした．

では、なぜランダムに選ぶのかを理解するには、最急勾配法の問題点を考える必要があります．最急降下法では、適当に選んだ初期パラメータから、ちょっとずつパラメータの更新を行いました．しかし、もし下図のような誤差関数があった場合、初期パラメータの選び方によっては、誤った解に収束してしまいます．

f:id:shirakonotempura:20190214092749p:plain

一方、SDGは、初期値に依存せずに最適パラメータを探すことになりますので、局所解に落ち込むリスクは最急降下法よりは小さいと言えます．

一般的にSDGは最急降下法より優れているみたいなので、SDGを使えば問題ないんだろうとは思いますが、一応以下にメリット・デメリットを上げておきます．

メリット
- 一方向から探す解を探すわけではないので、局所解に落ち込みにくい
- 全データを必要としないので、データを取りながらのオンライン学習に使える
- 計算が早い（らしい．これは実感していないのでわかりませんが、収斂回数は増えるけど、一回の計算に使うデータが１つなので、結果的に早くなるようです）．
デメリット
- ランダム性を含むので、最短では解にたどり着かない．
- 異常値があった場合、それに引っ張られやすい．（データを見てなんとかしましょう）

なお、最急降下法とSDGを組み合わせた、ミニバッチ勾配降下法（Mini Batch Gradient Descent）という方法が考えられています．これは最急降下法のように全データを使うわけではなく、いくつかのデータを選んで誤差関数を求める方法になります．

まとめ

関数近似における評価関数について、教師あり学習との比較を行いました
代表的な勾配法である最急降下法、確率的勾配降下法について整理しました

今回、評価関数 $E_{SE}(\boldsymbol{w})$ を示しましたが、真の価値関数を知ることはできませんので、この評価関数でパラメータの更新を行うことはできません．

次回はそのあたりの説明からはじめて、パラメータの更新について勉強して、整理したいと思います．

今回、以下の記事を参考にさせていただきました．ありがとうございました．

確率的勾配降下法の大雑把な意味 - 具体例で学ぶ数学

最急降下法のイメージと例 - 具体例で学ぶ数学

確率的勾配降下法とは何か、をPythonで動かして解説する - Qiita

2019-02-13

強化学習：関数近似（その１：導入）

強化学習関数近似

はじめに

今回から、Sutton本9章の内容について勉強しながら、関数近似についてまとめていきたいと思います．Sutton本では、この章（9章）からは第2部となっており、これまでTabular（表形式）で扱っていた状態を関数近似によって拡張していく内容になります．

これまでの場合、『状態、行動』が与えられたら、それに対応する『報酬、次の状態』をTableから選んで返すということができたわけですが、格子世界のような限られた状態に落とし込める問題というのは、現実にはそこまで多くありません。仮にあったとしてもその状態数が多かった場合、すべてを表形式で扱うことには限界がありそうなことは何となくイメージできるかと思います．

そこで状態評価や戦略をパラメータを持った関数で近似的に表してしまうことで、表では表現できなかった連続的な状態を表現することが可能になってきます．また、この関数近似によって強化学習とニューラルネットが結びつき深層強化学習（Deep Reinforcement Learning）に繋がっていくことになります．

f:id:shirakonotempura:20190213033052p:plain

ニューラルネットワークの説明に関しては、ここでは行いませんので以下の記事を参考にされてください． Chainerで始めるニューラルネットワーク - Qiita

pythonでニューラルネットワーク実装 - Qiita

【入門向け】ニューラルネットワークの仕組みを緩く図解 - Qiita

価値関数の近似

では、価値関数を近似するということを具体的にみていきます．

これまで価値関数は、状態価値 $V(s)$ や行動価値 $Q(s,a)$ という表現をしてきました．
くどいですが、関数近似のイメージを掴むため２×２の格子世界を考え、それぞれの状態価値 $V(s)$ を下記左図のように仮定します．ここでは、状態価値の関数近似をイメージしてます．
これを横軸に状態 $S$ 、縦軸に状態価値 $V(s)$ として無理やりグラフに落とし込みます（下図中央）．

この状態 $S$ と状態価値 $V(s)$ の関係性をパラメータ $\boldsymbol{w}$ を使って関数にしてしまうことで、テーブル表現だった価値関数を（近似）関数で表してしまおうというのが関数近似となります．先にも書いたように、このような関数の形で表現することで、離散的（とびとび）にしか扱えなかった状態や状態価値を、連続値として評価することが可能になります．

f:id:shirakonotempura:20190213034441p:plain

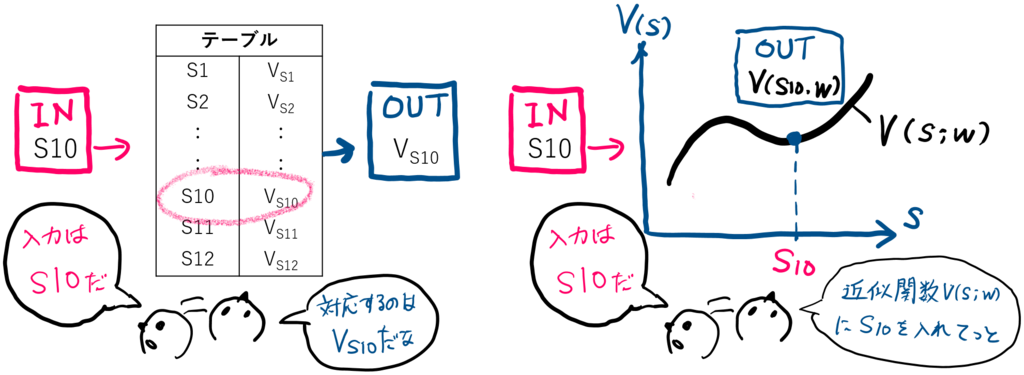
関数近似（Function Approximation）の種類

上のイメージ図は、状態 $S$ を入力として状態価値 $V(s)$ を推定する近似関数を例として表しましたが、関数近似は入力と出力の対象によって大きく3種類に分けることができます．

状態 $s$ を入力にして、状態価値を関数 $\hat{v}(s,\boldsymbol{w})$ で表す
状態 $s$ と行動 $a$ を入力にして、行動価値を関数 $\hat{q}(s, a, \boldsymbol{w})$ で表す
状態 $s$ を入力にして、行動 $a_m$ の数だけ行動価値を関数 $\hat{q}(s, a_m, \boldsymbol{w})$ で表す．

f:id:shirakonotempura:20190213035604p:plain

David Silver, UCL講義ノート: Value Function Approximationより

関数近似に用いる関数について

近似関数はパラメータ $\boldsymbol{w}$ を使って関数 $\hat{v}(s,\boldsymbol{w})$ や $\hat{q}(s, a, \boldsymbol{w})$ のように表すと書きましたが、実際は近似のベースになる関数は決めてあげる必要があります．このベースとなる関数は基底関数と呼ばれ、 $\phi(x_{i})$ で表されます．

基底関数の決め方にはルールはありませんので、基本的にどんな関数を使ってもいいのですが、以下に代表的なものを2つ紹介しておきます．

- 多項式基底： $$\phi_i (x) = x^i (i=0, 1, \cdots,M - 1) $$ 多項式基底では関数を多項式で表すことになります．

- ガウス基底： $$\phi _i (x) = exp\biggl[-\frac{(x - \mu_{i})^2}{2s ^2}\biggr] (i=1, \cdots,M) $$ ガウス基底は、平均 $\mu$ および標準偏差 $s$ を選んで定義します．正規分布と同じ釣り鐘状の関数を表現します．

近似関数はパラメータ $\boldsymbol{w}$ を調整しさえすれば、あらゆる形状が表現できる関数が望ましいのですが、１つの基底関数での表現力はその式の形状でしかありません．そのため、実際は基底関数を複数組み合わせることで、近似関数の表現力を高めてやる必要があります．

以下に、ガウス基底を使った近似関数の例を示します．左図が１つのガウス基底によるもので、右図が９つのガウス基底を使ったものになります．左図がガウス基底（正規分布）の形状しか表せていないのに対して、右図の関数はかなりの表現力を持っていそうなことがイメージできるかと思います．（この例では、パラメータ $\boldsymbol{w}$ によって各山の高さが変わります．）

f:id:shirakonotempura:20190213055038p:plain

今さら聞けない強化学習(11) 線形関数による価値関数近似 - Qiitaより引用

まとめ

内容に収集がつかなくなってきましたので、一旦終わります．

関数近似の概要を整理しました．

関数近似に関しては、もう2回くらいかけて

勾配降下法について内容
パラメータの更新

などについて整理したいと思います．